Factoriser avec la méthode de Horner

Si le réel a est une racine du polynôme f alors il existe un polynôme g tel que pour tout réel x :

f(x) = (x - a) . g(x)
La méthode de Horner est une sorte d'algorithme qui à partir des coefficients du polynôme f permet d'obtenir ceux du polynôme g. Illustration :

On appelle a0, a1, a2, ... an-1 et an les coefficients du polynôme f. Donc :

f(x) = an.xn + an-1.xn-1 + ... + a2.x2 + a1.x + a0
Si f est un polynôme de degré n alors g est nécessairement un polynôme de degré n-1.
On appelle b0, b1, b2, ..., et bn-1 ses coefficients. Ainsi :
g(x) = bn-1.xn-1 + ... + b2.x2 + b1.x + b0
Notre objectif est de lié les coefficients bk aux coefficients ak.

La seule relation que nous ayant entre les polynômes f et g est que pour tout réel x :

f(x) = (x - a) . g(x)
Développons (x - a) . g(x) :
(x - a) . g(x)2 = (x - a) .(bn-1.xn-1 + bn-2.xn-2 +... + b2.x2 + b1.x + b0)
= bn-1.xn + bn-2.xn-1 + ... + b2.x3 + b1.x2 + b0.x
    - bn-1.a.xn-1 - bn-2.a.xn-2 - ... - b2.a.x2 + b1.a.x + b0.a
= bn-1.xn + (bn-2 - bn-1.a).xn-1 + .... + (bk-1 - bk.a).xk + ...
    + (b1 - b2.a).x2 + (b0 - b1.a).x - b0.a

Or les polynômes f et (x - a) . g(x) sont égaux.
Comme deux polynômes égaux ont des coefficients égaux, on peut donc écrire que :

Pour xn, an = bn-12   donc  2 bn-1 = an2
Pour xn-1, an-1 = bn-2 - bn-1.a2   donc  2 bn-2 = an-1 + bn-1.a2
Pour xk, ak = bk-1 - bk.a2   donc  2 bk-1 = ak + bk.a2
Pour x2, a2 = b1 - b2.a2   donc  2 b1 = a2 + b2.a2
Pour x1, a1 = b0 - b1.a2   donc  2 b0 = a1 + b1.a2
Pour x0, a0 = - b0.a2   donc  2 b0 = -a0/a   si a est non nul...2

 

Appliquons par exemple, ceci au polynôme :

f(x) = 2.x4 - 5.x3 + 5.x2 - 7.x + 2
Ainsi ici :
a4 = 2   a3 = -5   a2 = 5   a1 = -7   a3 = 2

Une racine de ce polynôme f est le réel a = 2.
Donc il existe un polynôme   g(x) = b3.x3 + b2.x2 + b1.x + b0 tel que pour tout réel x :

f(x) = (x - a) . g(x)

De plus, d'après ce que nous venons de faire, nous pouvons dire que :

b3 = a4
b2 = a3 + b3.a 		b1 = a2 + b2.a
b0 = a1 + b1.a

Ces relations sont les rouages de la méthode de Horner...
Reportons les coefficients des deux polynômes dans un tableau :

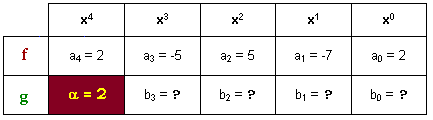
Ce tableau très ergonomique va permettre la poursuite de la manoeuvre...

Tout est à présent prêt. La méthode de Horner peut être lancée et appliquée. C'est l'objet de l'animation suivante :

La méthode de Horner en action...

Cliqu'moi d'ssus ! L'applette de Horner permet de factoriser n'importe quel polynôme suivant la méthode du même nom !
A condition toute fois d'en connaître une racine...
Suffit d'cliquer !

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Septembre 1999/Janvier 2003. Tous droits réservés.