
Toutes les fonctions ne prennent pas leur source à l'infiniment négatif pour se jeter à l'infiniment positif. Certaines fonctions n'existent qu'à partir d'un certain réel a sans y être nécessairement définie. Il est alors utile de regarder ce qu'il advient de la fonction lorsque l'on se rapproche de ce réel a. C'est la notion de limite en un point.
Limites en un point
Limite infinie en un point.
Par exemple, considèrons la fonction f définie sur l'intervalle ]3 ; +¥[ dont la courbe représentative est :

Observons de plus près cette courbe lorsque x se rapproche de 3.
 |
Lorsque x se rapproche de 3, f(x) devient de plus en plus grand sans qu'aucun plafond ne l'arrête.
On dit alors que f(x) tend vers +¥. Ou que la limite de la fonction f lorsque x tend vers 3 est égale à +¥. Ce que l'on résume par :  |
Note : Lorsque x se rapproche de 3, la courbe de la fonction f se rapproche de plus en plus de la droite D d'équation x = 3.
On dit alors que D est une asymptote verticale à la courbe de f au voisinage de 3.
Parmi les fonctions déjà vues en Seconde qui ont pour limite +¥ lorsque x tend vers a :
|
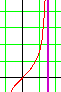 |
|
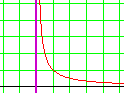 |
Nous avons exclusivement évoqué des fonctions qui tendent vers +¥ à l'approche d'un point. Mais il existe aussi des fonctions qui ont pour limite -¥.
C'est à peu près pareil, sauf qu'au lieu de s'envoler vers le ciel elles s'enfoncent dans les abysses...
 Pour l'instant, la seule approche que nous ayons donnée d'une limite infinie est une approche graphique. Mais il est possible de caractériser par une condition le fait qu'une fonction tende vers l'infini lorsque x tend vers 3 comme avec notre exemple...
Pour l'instant, la seule approche que nous ayons donnée d'une limite infinie est une approche graphique. Mais il est possible de caractériser par une condition le fait qu'une fonction tende vers l'infini lorsque x tend vers 3 comme avec notre exemple...

De manière plus générale, la définition d'une limite infinie d'une fonction en un point a est la suivante :

Limite à gauche et limite à droite.
Rappelez-vous : dans le paragraphe précédent, nous vous annoncions que la fonction inverse avait pour limite +¥ en 0. A présent, nous devons l'admettre et révéler la terrible vérité :

Dans ce qui suit, f désignera la fonction inverse. Ainsi pour tout x :
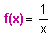
La fonction inverse f est définie sur l'intervalle ]-¥ ; 0[ È ]0 ; +¥[.
Autrement écrit, lorsqu'elle tend vers 0, elle peut le faire :

Examinons ces deux possibilités :
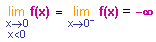

La fonction inverse n'admet pas de limite en 0. Certes elle a :
Par contre, pour la fonction g définie pour tout x par :

A l'instar de la fonction inverse, cette fonction g est définie sur ]-¥ ; 0[ È ]0 ; +¥[.
Sa courbe représentative aux abords de 0 est la suivante :
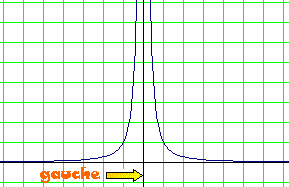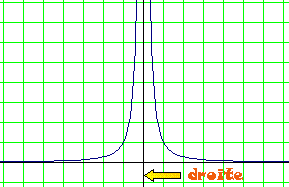
D'après cette courbe, on peut dire que :


Limite finie en un point.
Toutes les fonctions non définies en un point ne s'en vont pas vers les infinis. Certaines se dirigent vers un point précis. On dit alors que leur limite est finie.
Intéressons-nous à la limite en 0 de la fonction f définie pour tout x par :

Pour que f(x) existe, il faut que x passe l'épreuve de la racine et celle de l'inverse. Autrement écrit, il doit être positif et non nul
Donc son ensemble de définition est ]0 ; +¥[.
L'approche se fera donc exclusivement par la droite.
Pour avoir une idée de sa limite en 0, traçons la courbe représentative de f.
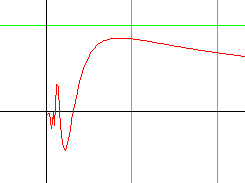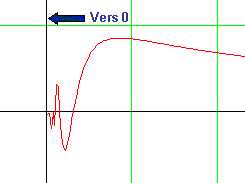 |
Lorsque x se rapproche de 0, f(x) se rapproche de plus en plus de 0.
On dit alors que la limite de la fonction f lorsque x tend vers 0 est égale à 0. On résume cela par :  |
| Prolongement par continuité.
On pourrait croire que tou s'arrête avec cette limite en 0. Que neni ! Car certains petits malins pourraient poser la question :
C'est vrai la fonction f n'est définie que sur l'intervalle ]0 ; +¥[. Donc elle n'est pas définie en x = 0.
Si f n'est pas définie en x = 0, on peut cependant l'y prolonger par continuité.
|
Un autre cas est celui de la fonction f(x) =  en 0. en 0.
Cette limite est un grand classique de la Première S... |
 Pour l'instant, la seule approche que nous ayons donnée d'une limite finie en un point est une approche graphique. Mais il est possible de le caractériser par une condition.
Pour l'instant, la seule approche que nous ayons donnée d'une limite finie en un point est une approche graphique. Mais il est possible de le caractériser par une condition.
La définition d'une limite finie d'une fonction en un point a est la suivante :

Sans limite !
Il existe des fonctions non définies en un point qui n'admettent aucune limite. Ainsi en va-t-il des fonctions suivantes :


Lorsque x se rapproche de 0, la fonction f s'affole. Elle oscille de plus en plus vite...
Ce qui explique les deux barres verticales rouges sur le graphique ci-contre autour de 0.
En 0, la fonction f n'a aucune limite possible...