 |
Un exemple type de limite finie en un point est le cas de la fonction sin(x)/x en 0. Elle n'y est pas définie pourtant elle y admet une limite. C'est toute l'histoire de ce qui suit... |
|
Un exemple type de limite finie en un point est le cas de la fonction sin(x)/x en 0. Elle n'y est pas définie pourtant elle y admet une limite. C'est toute l'histoire de ce qui suit... |
On considère la fonction f définie pour tout réel x non nul par :
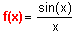
| Comme toute bonne pièce, cette aventutre comportera plusieurs actes : |
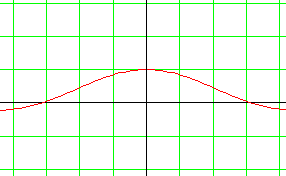
Il semblerait donc que lorsque x tend vers 0, f(x) tende vers 1.
Démontrons par le calcul, cet état de fait !
On considère sur le cercle trigonométrique la situation géométrique suivante :
 |
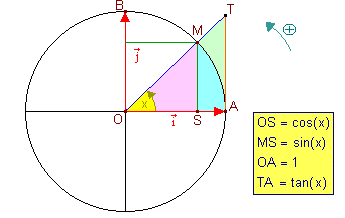Le point M est le point du cercle trigonométrique associé au réel x.
T est le point d'intersection de la droite (OM) et de la tangente au cercle trigonométrique en A. Bref, tout cela c'est du déjà vu ! |
On remarque que le triangle (OMS) est contenu dans la portion de disque (OMA) qui est lui même se trouve lui-même inclus dans le triangle (OTA).
Donc leurs aires sont rangées dans le même ordre.
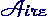(triangle (OMS)) £ (portion de disque (OMA)) £ (triangle (OTA))
Autrement écrit :
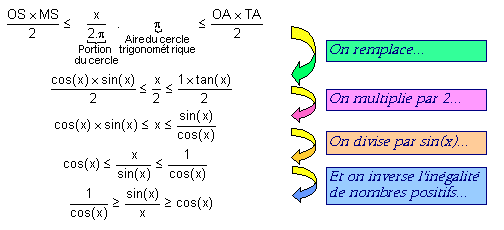
Conclusion : ainsi donc pour tout réel 0 < x < 
/2 :
Or lorsque x tend vers 0+ :
Ainsi donc :
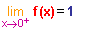
La fonction f a une propriété intéressante : elle est paire.
En effet, pour tout réel x non nul :
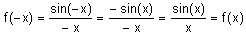
Ainsi :
Lorsque x tend vers 0-, alors -x tend vers 0+.
Or si -x tend vers 0+ alors f(-x) tend vers 1.
Vu que f(x) = f(-x), alors :
En conclusion :
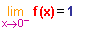
Conclusion : lorsque x va vers 0, f(x) = 
tend vers 1.
 |
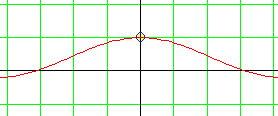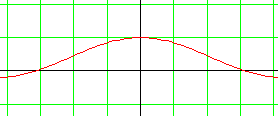La fonction f est donc prolongeable par continuité en 0. Il suffit juste de poser :
Son ensemble de définition est désormais ]-¥ ; +¥[. |
