ce qui suit est réservé à tous ceux qui refusent l'action de l'ignorance. La continuité ne disparaîtra pas comme Carthage...

L'aventure continue...

Ces dernières années, la continuité et les fonctions qui le sont, sont tombées en désuétude car tous les cas que l'on étudie le sont. A force de vivre sans risque, on finit par oublier qu'ils existent...
Il nous a paru utile et nécessaire de remettre ce concept en valeur.
Nous en donnerons de la continuité une vision graphique, puis une vision plus analytique.

Continuité : une vision graphique.
Graphiquement, une fonction continue est une fonction qui n'a aucun trou ou aucun décrochement sur son ensemble de définition. Par exemple :

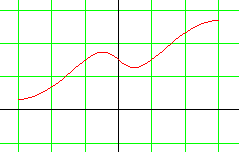
Ces deux fonctions sont définies sur l'intervalle [-3 ; 3]
Cette fonction est continue en x = 1.	Cette fonction n'est pas continue en x = 1. En effet, la courbe décroche en ce point.

En règle générale, toutes les fonctions vues sont continues sur leurs ensembles de définition respectifs. Ainsi :

1. les fonctions affines, les polynômes, sinus, cosinus et exponentielle sont continues sur R.
2. la fonction racine est continue sur [0 ; +¥[.
3. la fonction inverse est continue sur ]-¥ ; 0[ È ]0 ; +¥[.
4. la fonction logarithme est continue sur  ]0 ; +¥[.
5. la fonction tangente est continue sur ]-p/2 ; p/2[.

Ces fonctions n'ont aucun décrochement, ni aucun trou dans leurs courbes respectives.
C'est parce que quasiment toutes les fonctions étudiées au Lycée sont continues que l'on ne parle plus de continuité.
En résumé, retenez qu'une fonction continue est une fonction dont la courbe est sans trou ou sans décrochage sur son ensemble de définition.

Continuité : une vision analytique.
D'un point de vue plus analytique, pour définir la notion de continuité, on utilise la notion de limite en un point. Illustration avec ce qui suit :

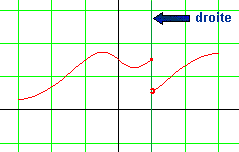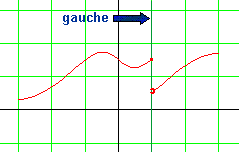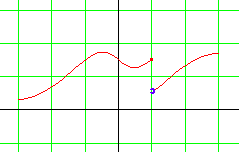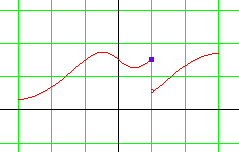
Observons le décrochage ci-contre. La fonction f ci-contre est définie sur l'intervalle [-3 ; 3]. Elle est donc définie en 1. D'ailleurs f(1) vaut 1,5. Lorsque x tend vers 1 par la gauche, f(x) tend vers 1,5 autrement écrit f(1). Lorsque x tend vers 1 par la droite, f(x) tend vers 0,6. Sa limite n'est pas f(1). C'est pour cela que la fonction f n'est pas continue en x = 1.

De cette constatation, découle la définition suivante :

Ainsi donc, pour démontrer qu'une fonction est continue en un point, il suffit de s'intéresser à sa limite en ce point.

Un problème de continuité est avant tout un problème de limite en un point...

Pour conclure, sachez qu'une fonction est continue sur un ensemble si elle est continue en chacun de ses points...

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Décembre 1998/Janvier 2003. Tous droits réservés.