Dans les exemples donnés dans cette page pour illustrer chaque cas, figurent les fonctions exponentielle et logarithme. Elles ne sont vues qu'en Terminale comme certains cas que nous aborderons. Mais ici, seules leurs limites sont intéressantes ! Dans les exemples donnés dans cette page pour illustrer chaque cas, figurent les fonctions exponentielle et logarithme. Elles ne sont vues qu'en Terminale comme certains cas que nous aborderons. Mais ici, seules leurs limites sont intéressantes !
Opérations sur les limites
Déterminer la limite d'une somme, d'un produit ou d'un quotient de fonctions ne consiste pas seulement à additionner ou à multiplier deux réels. En effet, une limite n'est pas nécessairement un réel. Elle peut être un infini ou ne pas exister.
Dans cette page, nous parlerons de:
 la limite d'une somme. la limite d'un quotient. |
la limite d'un produit. la limite d'une fonction composée. |
Nous allons envisager tous les cas possibles et inimaginables. Nous verrons que parfois, il n'y a pas de réponse générale.
Dans les trois tableaux ci-dessous, les limites sont considérés en un même endroit.
Limite d'une somme
De manière générale, la limite de la somme de deux fonctions est égale à la somme des limites de celles-ci. Sauf cas particuliers !
Enonçons les différents cas possibles :
|
Limite de f |
Limite de g |
Limite de f + g |
Par exemple... |
| l | l' | l + l' |  |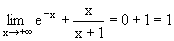
| l | +¥ | +¥ |  |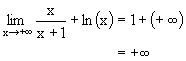
| l | -¥ | -¥ |  |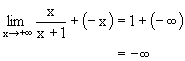
| +¥ | +¥ | +¥ |  |
| -¥ | -¥ | -¥ |  |
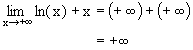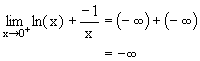| +¥ | -¥ | Indéterminé |  |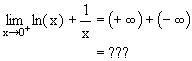
En conclusion, seul un choc de titans conduit à une indétermination. D'un infini face à un autre, lequel va gagner ?
Vous trouverez la réponse en creusant le problème...
Limite d'un produit.
A la différence de la somme, le produit de deux réels négatifs ne donnent pas un machin négatif.
En règle générale, la limite d'un produit est égale au produit des limites.Hors cas particuliers bien sûr !
Envisageons les différents cas possibles :
| Limite de f |
Limite de g |
Limite de f . g |
Par exemple... |
| l | l' | l × l' |  |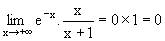
| l positif non nul |
+¥ | +¥ |  |
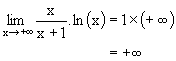| l positif non nul |
-¥ | -¥ |  |
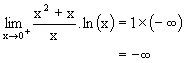| l négatif non nul |
+¥ | -¥ |  |
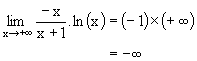| l négatif non nul |
-¥ | +¥ |  |
| +¥ | +¥ | +¥ |  |
| +¥ | -¥ | -¥ |  |
| -¥ | -¥ | +¥ |  |
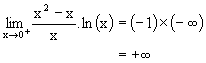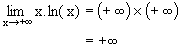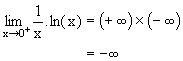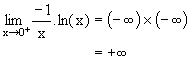| 0 | -¥ ou +¥ | Indéterminé |  |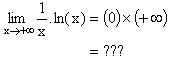
En conclusion, seul un choc de genre David Zéro vs. Goliath Infini conduit à une indétermination. De l'infiniment petit ou de l'infiniment grand, lequel l'emportera ?
Pour déterminer la limite, il faut donc creuser un peu plus le problème...
Limite d'un quotient.
Aux histoires de signe de la multiplication, la division ajoute le fait qu'on ne peut pas diviser par 0.
Cela se retrouve dans les différents cas possibles de limites. Examinons-les.
| Limite de f |
Limite de g |
Limite de f / g |
Par exemple... |
| l | l' non nul |
 |
 |
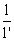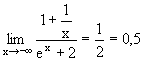| l | -¥ ou +¥ | 0 |  |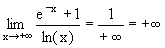
| +¥ | l' positif non nul |
+¥ |  |
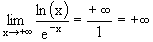| +¥ | l' négatif non nul |
-¥ |  |
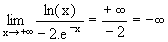| -¥ | l' positif non nul |
-¥ |  |
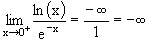| -¥ | l' négatif non nul |
+¥ |  |
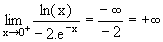| -¥ ou +¥ | -¥ ou +¥ | Indéterminé |  |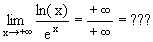
| l positif non nul ou +¥ |
0 en restant positif |
+¥ |  |
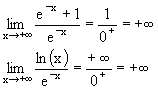| l positif non nul ou +¥ |
0 en restant négatif |
-¥ |  |
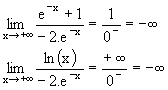| l négatif non nul ou -¥ |
0 en restant positif |
-¥ |  |
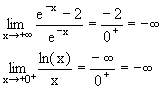| l négatif non nul ou -¥ |
0 en restant négatif |
+¥ |  |
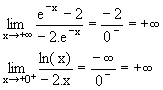| 0 | 0 | Indéterminé |  |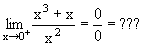
En conclusion, seuls les chocs de deux mêmes extrêmes (deux infinis ou deux zéros) conduit à une indétermination.
Entre deux infiniment grands ou entre deux infiniment petits, le problème demeure ?
Pour déterminer la limite, il faut donc poursuivre les investigations...
Limite d'une fonction composée.
Le théorème qui suit est assez naturel. Néanmoins, la rigueur qui caractérise tout mathématicien encroûté impose qu'on l'énonce !
Par exemple, avec la fonction f définie par tout réel x par :
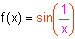
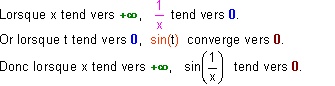
Ainsi :
