Le théorème suivant est enseigné en Première. Il est rare que
l'on voit sa démonstration. Même si elle n'est pas d'une redoutable difficulté, elle n'est seulement abordée qu'après le BAC...
|
Le théorème suivant est enseigné en Première. Il est rare que
l'on voit sa démonstration. Même si elle n'est pas d'une redoutable difficulté, elle n'est seulement abordée qu'après le BAC... |
| Théorème : f est une fonction dérivable sur
l'intervalle ]a ; b[. x0 est un réel de cet intervalle.
Si f admet un maximum ou un minimum local en x0 alors f'(x0) = 0. |
La preuve de ce théorème :
Nous traiterons seulement le cas d'un maximum local. En effet, la
démonstration pour un minimum local ressemble à ce que nous ferons.
Ce que nous savons :
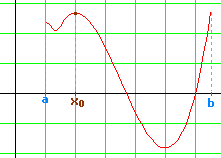
Pour prendre un exemple, nous avons graphiquement la situation suivante ci-contre : |
 |
 |
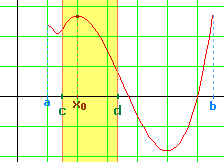Comme f admet un maximum local en x0
alors il existe un intervalle [c ; d] autour de x0 sur lequel f(x) 
f(x0)
Donc pour tout réel x de l'intervalle [c
; d], on a f(x)
- f(x0)
|
Nous savons que la fonction f est
dérivable sur l'intervalle ]a ; b[.
Elle l'est donc en x0.
Donc lorsque x tend vers x0, le
quotient 
tend vers f'(x0).
Mais on peut tendre x0 vers par la gauche ou par la droite. Examinons les deux cas :
 |
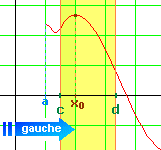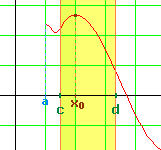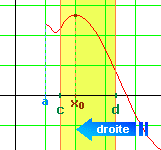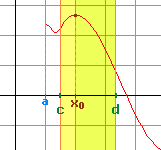
Cas 1 : Lorsque x se trouve entre c
et x0, il est clair que x
- x0 est négatif. Donc le quotient
est positif ou nul.
Donc la limite de ce quotient positif ou nul
lorsque x tend vers x0,
est elle-aussi positive ou nulle. |
| Cas 2 : De même, lorsque x se trouve entre x0
et d, la différence est positive. Donc le quotient
est là négatif ou nul.
Donc la limite de ce quotient négatif ou nul
lorsque x tend vers x0,
est elle-aussi négative ou nulle. |
 |
Récapitulons ce que nous avons trouvé sur f'(x0). Nous savons que :
Pour que f'(x0)
remplisse ces deux conditions, il n'y a qu'une seule possibilité : il doit
être égal à 0.
Donc f'(x0)
= 0.
D'où le théorème.
0.