Les fonctions à dériver sont des sommes, des différences, des produits, des quotients ou des composées de fonctions dont on connaît déjà les dérivées.
Nous allons voir les théorèmes et les formules qui permettent de différencier ces premières. Le tout sera illustré par une flopée d'exemples...

 

Dérivée du produit d'une fonction par un réel.
La dérivation se marie très bien avec le produit par un réel. A ne pas confondre avec le produit avec une autre fonction que nous verrons plus tard...

Théorème : On suppose que u est une fonction dérivable en x. l est un nombre réel.
Si ces conditions sont remplies alors :

  • La fonction  l.u  est dérivable en x.

  • Le nombre dérivé au point x de la fonction l.u  est égal au produit de l  et du nombre dérivé de u au point x.

Autrement écrit :

(l.u)' (x) = l . u'(x)

Par exemple, déterminons la dérivée de la fonction f(x) = 7.x5.
La dérivée de la fonction x5 est égale à  5.x4 . D'où :

f'(x) = (7.x5)' = 7 . (x5)' = 7 . (5.x4) = 35.x4

 

Dérivée d'une somme.
Dériver la somme de deux fonctions n'est guère compliqué. La preuve avec ce qui suit :

Théorème : u et v sont deux fonctions dérivables en x.
Si ces deux conditions sont remplies alors :

  • La fonction  u + v est dérivable en x.

  • Le nombre dérivé au point x de la somme u + v est la somme des nombres dérivés de u et v au point x.

Autrement écrit :

(u + v)' (x) = u'(x) + v'(x)

La preuve

Par exemple, déterminons la dérivée de la fonction f(x) = 7.x3 - 3.x2 + 3.
Les dérivées des fonctions x3, x2 et 3 sont respectivement 3.x2, 2.x et 0.
Ainsi :

2f '(x)

= (7.x3 - 3.x2 + 3)'
= (7.x3)' - (3.x2)' + (3)'
= 7 . (x3)' - 3 . (x2)' + (3)'
= 7 . (3.x2) - 3 . (2.x) + 0
= 21.x2 - 6.x


Dérivée d'un produit.
Contrairement à la somme ou au produit par un réel, le produit de deux fonctions passe assez mal le cap de la dérivation...

Théorème : u et v sont deux fonctions dérivables en x.
Si ces deux conditions sont remplies alors :

  • La fonction u.v est dérivable en x.

  • Le nombre dérivé au point x du produit u.v est égal à  u(x) . v'(x) + u'(x) . v(x).

Autrement écrit :

(u.v)' (x) = u(x) . v'(x) + u'(x) . v(x)

La preuve

Par exemple, déterminons la dérivée de la fonction  f(x) = (x3 - x +1) . (x2 - 1).
Pour calculer la dérivée de cette fonction f, on a le choix entre un développement fastidieux ou appliquer notre formule. Inutile de préciser que la seconde option est la moins pénible...
La fonction f est le produit des fonctions :

On peut donc écrire que :

2f '(x)

= u(x) . v'(x) + u'(x) . v(x)
= (x3 - x +1) . (2.x) + (x2 - 1) . (3.x2 - 1)
= 2.x4 - 2.x2 + 2.x + 3.x4 - x2 - 3.x2 + 1
= 5.x4 - 6.x2 + 2.x + 1 

Il n'est pas certain que développer f n'eut pas constituer une meilleure option. Sauf que l'on aurait pas illustrée cette propriété...

 

Dérivée de l'inverse d'une fonction.
N'importe quelle fonction peut être inversée pour peu qu'elle ne s'annule pas.
Sous cette condition et sous d'autres, il est possible de dériver l'inverse d'une fonction.

Théorème : u est une fonction dérivable en x. On suppose également que u(x) est non nul.
Si ces deux conditions sont remplies alors :

  • La fonction 1/u est dérivable en x.

  • Le nombre dérivé au point x de 1/u est égal à .

Autrement écrit :

La preuve

Par exemple, déterminons la dérivée de la fonction f(x) = . 
Cette fonction est l'inverse de la fonction  u(x) = x2 + 1 dont la dérivée est 2.x.
Ainsi :

Nous l'avons à maintes fois dit et répété : une division est une multiplication par l'inverse.
La formule de la dérivée de l'inverse préfigure et permet de démontrer celle du quotient que voici.

 

Dérivée d'un quotient.
"Diviser revient à multiplier par l'inverse". C'est sur cet adage que repose le théorème suivant : sur la dérivation d'un produit et sur celle de l'inverse d'une fonction.

Théorème : u et v sont deux fonctions dérivables en x. On suppose également que v(x) est non nul.
Si ces trois conditions sont vérifiées alors :

  • La fonction  u/v  est dérivable en x.

  • Le nombre dérivé au point x du quotient u/v est égal à  .

Autrement écrit :

La preuve

Par exemple, déterminons la dérivée de la fonction f(x) = .
La fonction f est le produit des fonctions :

On peut donc écrire que :

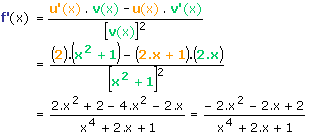
Lors du développement du numérateur, il convient de faire attention au signe moins qui exerce son influence négative sur tout le produit  (2.x + 1) . (2x)...

 

Réservé aux élèves de Terminale... Dérivée d'une fonction composée.
Nous avons abordé la composition lorsque nous avons parlé des opérations qui pouvaient être pratiquées sur les polynômes. Nous en avons reparlé à l'occasion des limites.
En tout cas, une chose est sûre : même une fonction composée peut être dérivée sous certaines conditions...

Théorème : f est une fonction dérivable en x. g est une fonction dérivable en f(x).

Si ces deux conditions sont réunies alors :

  • La fonction  g o f  est dérivable en x.

  • Le nombre dérivé au point x de la fonction composée  g o f  est égal à  
    f'(x) . g'(f(x)).

Autrement écrit :

(gof)' (x) = f'(x) . g'( f(x) ) 

La preuve

Par exemple, intéressons-nous à la fonction f(x)= sin(3.x2 + 1).
Elle est la composée de deux fonctions dérivables sur R que sont :

Comme f(x) = v(u(x)), on peut donc écrire que :

2f '(x)

= u'(x) . v'(u(x))
= (6. x) . cos(3.x2 + 1)
= 6.x . cos(3.x2 + 1)

Un autre exemple est la fonction  g(x) = .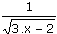
Pour calculer la dérivée de la fonction , nous pourrions recourir à la formule de dérivation de l'inverse. Mais nous allons faire autrement...
On peut dire que g est la composée des fonctions :

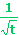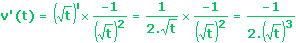
Tout est à présent prêt pour l'action finale. En effet :

 

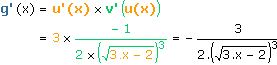
Des fonctions composées que l'on rencontre assez souvent lors des devoirs et autres sujets de BAC sont celles comportant de la fonction affine.
Elles sont de la forme f(a.x + b).
Les deux tableaux suivants donnent les dérivées des principales fonctions de ce genre.

Dérivées de composées avec une fonction affine :
Polynômes, racine et fonctions inverses

Fonction

Dérivée

Exemple
(a.x + b)n

n est positif		 n.a . (a.x +b)n-1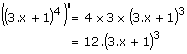


n est positif

Pour les scientifiques et les autres, il convient de rajouter le tableau suivant :

Dérivées de composées avec une fonction affine :
Logarithme, exponentiel, fonctions trigonométriques

Fonction

Dérivée

Exemple
sin(a.x + b) a . cos(a.x +b) ( sin(3.x+1) )' = 3. cos(3.x + 1)
cos(a.x + b) -a . sin(a.x +b) ( cos(3.x+1) )' = -3. sin(3.x + 1)
ea.x+b

a . ea.x+b

 ( e3.x+1 )' = 3 . e3.x+1
(a.x + b)a a . a . (a.x +b)a-1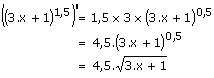

Une application directe et pratique de la dérivée d'une fonction composée concerne la dérivée d'une fonction réciproque. Elle n'est pas abordée au Lycée. Pourtant nous allons l'aborder...

 

A l'extrème limite du programme de Terminale... Dérivée d'une fonction réciproque.
La notion de fonction réciproque n'est pas au lycée un thème d'étude si ce n'est pour des cas particuliers comme le couple logarithme/exponentielle.

Quand on parle de réciproque, on parle généralement aussi d'injections, de surjections, de bijections. Autant de sujets sur lesquels la vérité peut vous être révélée.
 

Théorème : f est une fonction dérivable en x. 
On suppose que f admet au voisinage de x une fonction réciproque g.
On appelle y = f(x). Donc  g(y) = x

Si f' ne s'annule pas en x  alors  la fonction réciproque g est dérivable en y = f(x).
De plus :

La preuve

Par exemple, intéressons-nous à la fonction f définie pour tout réel positif x par :

f(x) = x2

Cette fonction f est une bijection de [0 ; +¥[ sur [0 ; +¥[. 
La réciproque de f est la fonction g définie pour tout réel positif y par :

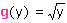
C'est du déjà vu !

En effet pour tout réel positif x :

Pour ceux qui n'en seraient pas convaincus, voir cliquer !

Calculons la dérivée de la réciproque g avec notre formule :
La dérivée de la fonction f est  f'(x) = 2.x.
Ainsi :

Autrement dit, une chose que l'on savait déjà !
Nous aurions pu être pertinent en vous parlant des réciproques des fonctions trigonométriques. C'est d'ailleurs l'objet d'une autre page ci-dessous !

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) Mai 2000/Janvier 2003. Tous droits réservés.