| Arc sinus : réciproque de la
fonction sinus.
Qui dit réciproque, dit bijection. Or,
la fonction sinus est tout sauf cela !
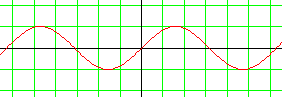 |
Il n'y a qu'à voir la courbe !
Comment peut-on être bijective avec une courbe pareille ? |
Par contre, si la fonction sinus
est restreinte à l'intervalle
[-p/2
; p/2]
alors elle le devient. |
 |
Restreinte, la fonction sinus est une
bijection de l'intervalle [-p/2
; p/2]
sur [-1 ; 1].
On peut donc lui trouver une fonction réciproque : on l'appelle Arc
sinus.
|
Arcsin : [-1
; 1]  [-p/2
; p/2] [-p/2
; p/2]
La courbe de
cette fonction s'obtient par symétrie par rapport à la
première bissectrice du plan : la droite d'équation y = x. |
 |
Intéressons-nous à la dérivabilité
de la fonction arc sinus.
Dérivabilité et
dérivée de Arc sinus.
Etant donné :
- que la fonction sinus est
dérivable sur tout l'intervalle
[-p/2
; p/2].
- que sa dérivée, la fonction
cosinus est
non nulle sur l'intervalle
]-p/2
; p/2[.
alors la fonction arc sinus est
dérivable sur ]-1 ; 1[.
Nous allons pouvoir calculer sa dérivée en utilisant la
formule adéquate.
Comme la dérivée de la
fonction sinus est cosinus alors :
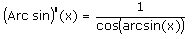
Et là, on est
bloqué !
En fait, ce qu'il faudrait, ce serait pouvoir transformer le
cosinus en quelque chose de plus "sinus".
Or lorsque a fait partie de l'intervalle [-p/2
; p/2],
on montre que :

Autrement dit, et
compte tenu que la fonction arc sinus abouti dans
l'intervalle
[-p/2
; p/2],
on peut écrire que :

|
Conclusion : la
fonction Arc sinus est dérivable sur ]-1 ; 1[ (elle n'est donc
pas dérivable en x =-1 et x = 1).
De plus, pour tout x Î ]-1 ; 1[ :
 |
|