| Le logarithme népérien est au programme de Terminale de toutes les séries abordant sérieusement les mathématiques. Parfois les propriétés ne sont qu'énoncées. Dans un souci de modernité et pour ne pas faire comme tout le monde, nous nous efforcerons d'aller au fond des choses : une belle étude à l'ancienne. |

le logarithme népérien
Les logarithmes constituent l'une des deux familles de fonctions introduites en Terminale. On aborde ces premières au travers de la plus éminente de ses représentantes : le logarithme népérien.
Définie comme étant une primitive de la fonction inverse, le logarithme népérien (appelez-le "ln") présente certaines propriétés singulières. Voici son histoire...
Nous ferons comme si la calculatrice n'existait pas, comme aux temps héroïques où tout était encore à découvrir...
Les fondements.
De toutes les fonctions inverses (comprenez une chose de la forme 1/puissance de x), seule la fonction f(x) =  n'avait pas de primitive évidente. Il fallut donc la créer : c'est ainsi que naquit le logarithme népérien.
n'avait pas de primitive évidente. Il fallut donc la créer : c'est ainsi que naquit le logarithme népérien.
| Définition du logarithme népérien.
Le logarithme népérien est la fonction notée ln et définie sur ]0 ; + |
Quelques remarques :
 .
. ; 0[ È ]0 ; +
; 0[ È ]0 ; + [, une primitive de
[, une primitive de 
La définition nous permet déjà de connaître les variations du logarithme népérien.
En effet, lorsque x est strictement positif alors il en va de même pour  .
.
Donc la fonction ln est strictement croissante sur l'intervalle ]0 ; + [.
[.
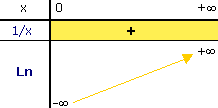
Son tableau de variation est donc le suivant :
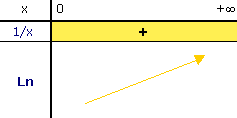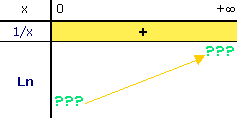
Note : nous savons que ln est toujours croissante mais nous ignorons d'où elle vient et vers quel horizon elle s'en va. En résumé, nous ignorons quelles sont ses limites en 0 et en + .
.
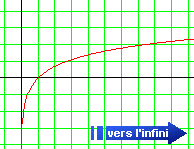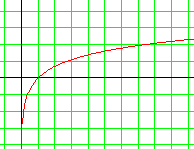
| La courbe de la fonction ln. Dans l'absolu avec ce que nous avons fait, il nous est impossible de tracer la courbe représentant la fonction ln. Seulement, il faut bien en parler ! Graphiquement, la fonction ln démarre ultra-vite : l'axe des ordonnées est une asymptote verticale à cette courbe en 0. Puis, plus on progresse, plus on grimpe lentement ! |
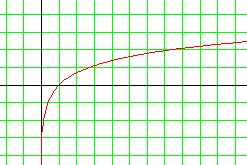 |
Les propriétés.
Le logarithme népérien a la particularité de transformer les produits en sommes, les quotients en différences et les puissances en multiplications. En cela, il fait mieux que Jésus. Voyons comment !
| Propriété : si a et b sont deux réels strictement positifs alors ln(a.b) = ln(a) + ln(b) | ||||||||||
Cette propriété sert dans les deux sens. Par exemple :
| ||||||||||
| La preuve : pour démontrer cette propriété, nous allons dériver séparément deux fonctions. Soit a un réel strictement positif.
Les fonctions et ont donc des dérivées égales. Elles sont donc deux primitives de la fonction Pour cela, calculons les images de 1 par ces deux fonctions.
Donc k = 0 et les fonctions g et h sont égales. Ainsi si a est un réel strictement positif alors pour tout réel b de , on a :
Autrement dit, ce que l'on voulait ! |
Les fonctions logarithmes sont les seules à savoir transformer les produits en somme.
Et quand on a cette propriété, il est bien rare qu'il n'y en ait pas d'autres qui concernent le quotient, la puissance ou la racine carrée...
Propriétés : Si a et b sont deux réels strictement positifs et
n est un entier alors :
| ||||||
Comme la première propriété, ces quatre-là permettent de débloquer des situations. Par exemple :
| ||||||
| La preuve de ces quatre propriétés : Nos quatre démonstrations reposent toutes sur la propriété du logarithme d'un produit. a et b sont deux réels strictement positifs et n est un entier relatif. Entamons la manoeuvre :
D'où la propriété iv. |
Ces cinq propriétés vont nous permettre de répondre à la question : quelles sont les limites en 0 et en + de la fonction ln.
de la fonction ln.
Elles peuvent aussi servir à déterminer certaines limites ou résoudre comme nous le verrons à la fin.
Deux limites pour un logarithme.
Dans ce paragraphe, nous allons intéresser aux limites de ln en 0 et en + .
.
Déterminons la limite de ln lorsque x s'en va + .
.
Nous savons que la fonction ln est croissante sur l'intervalle ]0 ; + [ et que ln(1) = 0.
[ et que ln(1) = 0.
Ces deux renseignements ne nous donnent pas pour autant la limite ln de lorsque x s'en va vers + .
.
| Au vu de sa courbe, la fonction ln peut très
bien ne pas dépasser un certain plafond. L'air de rien, elle peut tout
aussi bien croître vers l'infini à l'instar de la fonction racine.
En fait, une seule chose est sure : la fonction ln
admet une limite en + |
 |
Essayons de voir jusqu'où le logarithme népérien peut monter.
Pour y parvenir, revenons à la définition de ln. Nous savons qu'il s'agit de la primitive de  qui s'annule en x = 1. Exploitons ces deux renseignements !
qui s'annule en x = 1. Exploitons ces deux renseignements !
Sur l'intervalle [1 ; 2], on peut écrire que : 

![]()
 1.
1.
En application de l'inégalité des accroissements finis, on peut alors affirmer que :
 . (2 - 1)
. (2 - 1)  ln(2) - ln(1)
ln(2) - ln(1)  1 . (2-1)
1 . (2-1)

 ln(2)
ln(2)  1
1
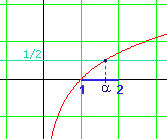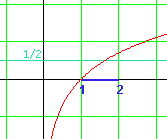
Cette inégalité signifie que ln(2) est compris entre  et 1.
et 1.
Mais elle signifie également que la fonction ln (qui est continue) passe la barre  lorsque x est compris entre 1 et 2. lorsque x est compris entre 1 et 2.
Donc il existe un réel a compris entre 1 et 2 tel que ln(a) = |
 |
C'est peut-être pas grand chose, pourtant c'est le début de tout !
Car le fait que ln atteigne  en signifie avec une certaine propriété que ln peut grimper aussi haut qu'elle le veut !
en signifie avec une certaine propriété que ln peut grimper aussi haut qu'elle le veut !
Soit M un réel positif quelconque.
La question est : la fonction ln grimpe-t-elle au dessus de l'altitude M ?
Appelons p le premier entier plus grand que 2.M.
On peut alors écrire que :
ln(a p) = p . ln(a)
Or p est plus grand que 2.M et ln(a) =  .
.
Donc :
| ln(a p) |  2.M . 2.M . |
| ln(a p) |  M M |
La fonction ln dépasse donc à un certain moment p l'altitude M.
Or nous savons que la fonction est strictement croissante donc : si x > p alors ln(x) > M.
En clair, nous venons de démontrer que :
Pour tout réel positif M, il existe un certain moment p à partir duquel ln(x) > M.
Quelque soit le plafond M que l'on fixe, il est à partir d'un certain moment p à jamais dépassé par ln.
ln(x) est donc une croissante non majorable. Donc lorsque x s'en va vers + , ln(x) tend aussi vers +
, ln(x) tend aussi vers + .
.
Certes, elle s'y rend à un rythme de sénateur mais elle y va inexorablement.
Théorème : la limite de ln(x) lorsque x tend vers + , est égale à + , est égale à + . .
|
Reste à déterminer la limite du logarithme népérien lorsque x tend vers 0. C'est la précédente limite qui va nous la donner.
Pour tout réel strictement positif x, on peut écrire que : ln(x) = - ln  .
.
| Donc lorsque x tend vers 0, | alors  tend vers + tend vers + |
alors ln  tend vers + tend vers + |
|
alors - ln  tend vers - tend vers - |
En conclusion, lorsque x tend vers 0, ln(x) s'enfonce vers l'infiniment négatif ou - .
.
Théorème : la limite de ln(x) lorsque x tend vers 0, est égale à - . .
|
L'axe des ordonnées est donc une asymptote à la courbe représentant la fonction ln au voisinage de 0.
Nous pouvons désormais compléter notre tableau de variation avec les deux limites qui manquaient. Ainsi donc :
Bijection.
Comme la fonction ln est strictement croissante sur l'intervalle ]0 ; + [ alors c'est une bijection de cet intervalle sur ]-
[ alors c'est une bijection de cet intervalle sur ]- ; +
; + [.
[.
La première conséquence de cela est que le logarithme népérien admet une fonction réciproque qui l'on appelle fonction exponentielle.
Ensuite, on peut affirmer que tout réel y0 a exactement un antécédent x0 par la fonction ln.
Donc deux réels strictement positifs a et b
ayant le même logarithme sont nécessairement égaux. Autrement écrit :
Si ln(a) = ln(b) alors a = b.
Cette dernière trouvaille est intéressante pour la résolution de certaines
équations. Voyons quelques exemples :
Il suffit de cliquer sur une équation ci-dessous pour avoir accès à sa
résolution...
|
ln(3.x + 1) = 0
ln(3.x + 1) = ln(2.x - 2)
ln | |||||||||||||||||
|
Résolvons l'équation ln(3.x + 1) = 0. On sait que l'antécédent de 0 par ln est 1. On peut donc écrire que :
Or deux réels strictement positifs ayant des logarithmes égaux le sont aussi.
| |||||||||||||||||
|
Résolvons l'équation ln(3.x + 1) = ln(2.x
- 2). Le début de la résolution sera le même que précédemment. Si les réels strictement positifs 3.x + 1 et 2.x - 2 sont des logarithmes égaux alors c'est qu'ils le sont. Ainsi :
La normalité voudrait que nous concluions : l'unique solution de cette équation est -3.
Où nous sommes-nous donc trompés dans notre résolution ? En fait, nous n'avons fait aucune erreur. Simplement, notre résolution est incomplète. En fin de résolution, la chose à est de vérifier qu'elle est bel et bien remplie. Il faut donc vérifier que les réels 3.x + 1 et 2.x - 2 sont bien strictement positifs. Sinon pas de logarithme. En fait, il faut vérifier que tout x trouvé ne fait pas capoter l'équation...
| |||||||||||||||||
Résolvons l'équation ln 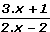 = 0. = 0.Et ça recommence toujours pareil !
Si les réels strictement positifs
Appliquons la bonne résolution prise à la seconde équation. Calculons
Comme 1 a bien un logarithme, nous pouvons alors en conclure que :
|
Des trucs en vrac.
Pour conclure cette page consacrée au logarithme, nous allons évoquer tout une série de chose qui découle de et qui nous semblent importantes : quelques trucs en vrac...
Au menu, il y aura :
Ca commence maintenant !
loga(x) = 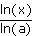
Ce logarithme en base a présente les mêmes propriétés produit-somme ou quotient-différence que ln.
Dans cette famille, c'est surtout le logarithme en base 10 aussi appelé logarithme décimale qui est le plus considéré et le plus employé. Notamment par les chimistes (le pH) et les physiciens.
Au lieu log10, on se contente souvent de la notation log.
Par exemple, intéressons-nous à la fonction f définie sur ]-0,5 ; + [ par :
[ par :
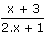
Nous allons faire les calculs des deux manières : la directe et l'"intelligente".
Enonçons au préalable la formule de la dérivée d'une composée logarithmique. Elle découle de la formule générale :
Proposition : Si u est une fonction dérivable et strictement positive sur un intervalle I alors :
|
| La méthode "directe" | La méthode intelligente | |
On dérive directement en utilisant la formule ci-dessus. Ici :
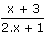
|
Avant de dériver, nous allons optimiser l'écriture de f(x) en utilisant la propriété quotient-différence de ln.
Pour tout réel x de l'intervalle ]-0,5 ; + 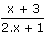 = ln(x+3) - ln(2.x+1) = ln(x+3) - ln(2.x+1)On peut alors écrire que :
|
La seconde méthode est plus économique en calculs. Elle requiert certes un peu d'astuce mais elle est très efficace au combat !
| Note : la méthode "intelligente" fonctionne ici car nous avions deux réels positifs en la personne de x + 3 et 2.x + 1. S'ils ne l'avaient pas été, nous n'aurions pas pu appliquer la propriété. |
Déterminons la limite en + de la fonction f définie sur ]-0,5 ; +
de la fonction f définie sur ]-0,5 ; + [ par :
[ par :
Examinons le problème de prime abord. Lorsque x s'en va vers + :
:
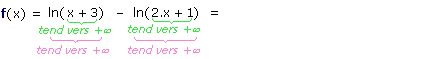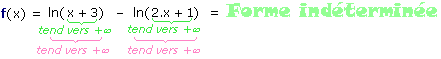
Pour (éventuellement) déterminer la limite de f(x) en + , nous allons devoir en modifier l'écriture.
, nous allons devoir en modifier l'écriture.
Pour cela, nous allons utiliser la propriété quotient-différence de ln.
Ainsi donc, pour tout réel x de l'intervalle ]-0,5 ; + [, on a :
[, on a :
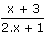
Or 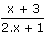 est ce que l'on appelle une fonction rationnelle.
est ce que l'on appelle une fonction rationnelle.
Donc à l'infini, 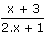 se comporte comme le quotient de ses deux termes dominants
se comporte comme le quotient de ses deux termes dominants 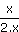 .
.
Ainsi lorsque x tend vers + , , |
le quotient 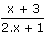 tend vers tend vers  . . |
donc ln 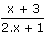 tend vers ln tend vers ln  = - ln(2) = - ln(2) |
Conclusion : la limite de ln(x) lorsque x tend vers + , est égale à - ln(2). , est égale à - ln(2). |