Dans le présent chapitre, nous outrepasserons le programme de Terminale. Le dernier paragraphe est en particulier largement hors-programme. C'est d'ailleurs qu'il est là !
| Les primitives ne sont abordées dans toutes les sections qu'en Terminale. Le principal usage qui en est fait, est le calcul d'intégrales. Dans le présent chapitre, nous outrepasserons le programme de Terminale. Le dernier paragraphe est en particulier largement hors-programme. C'est d'ailleurs qu'il est là ! |
Primitives story 1
le temps du commencement
Déterminer une primitive, c'est un peu comme chercher l'origine d'une dérivée.
Dans la présente page, nous définirons la notion de primitive puis nous aborderons celles des fonction de références et de certaines autres.
Le programme peut paraître peu ambitieux. Il est néanmoins copieux...
Définition primitive.
Chercher la primitive d'une fonction, c'est en quelque sorte dériver à l'envers...
| Définition : f est une fonction continue sur un intervalle I.
Dire que la fonction F : I ® R est une primitive de la fonction f signifie que :
Autrement écrit : F est une primitive de f équivaut à f est la dérivée de F. |
Pour bien saisir ce dont il s'agit, examinons quelques exemples.
 . sin(x2).
. sin(x2). . (x2)' . cos(x2) = x . cos(x2) = g(x).
. (x2)' . cos(x2) = x . cos(x2) = g(x).| Le truc à retenir : On prouve qu'une fonction F est la primitive d'une fonction f en démontrant que f est la dérivée de F. C'est ce que nous avons fait avec nos deux exemples. |  |
La primitive est tellement liée à la dérivation qu'elle en a adopté les qualités et les défauts. Ainsi :
| Primitive(u + v) = Primitive(u) + Primitive(v) |
| Primitive(u - v) = Primitive(u) - Primitive(v) |
| Primitive(l . u) = l . Primitive(u) |
| Primitive(u.v) n'est pas Primitive(u) . Primitive(v) |
| Primitive(1/u) n'est pas 1/Primitive(u) |
| Primitive(u/v) n'est pas Primitive(u)/Primitive(v) |
| Primitive(u o v) n'est pas Primitive(u) o Primitive(v) |
Car intégrer (comprenez déterminer une primitive) ou "primitiver" une fonction, ce n'est rien d'autre que dériver à l'envers...
| Remarque : à nous lire, on pourrait croire que seules les fonctions continues ont des primitives. La vérité est qu'elles ne sont pas les seules à en avoir. Par exemple, intéressons-nous à la fonction f définie par :
Pourtant elle admet une primitive en la personne de la fonction F définie par :
|
Primitives d'une même fonction.
Une fonction a au mieux une dérivée. Mais il en va différemment pour les primitives.
En effet, nous avons vu que les fonctions F(x) = x2 + x et F1(x) = x2 + x - 2 étaient deux primitives de la fonction f(x) = 2.x + 1.
Une fonction continue admet donc au moins deux primitives. Nous pourrions essayer de les compter. Mais ce serait sans doute un travail sans fin. Nous allons plutôt essayer de voir ce que deux primitives d'une même fonction ont en commun.
|
Ce que deux primitives d'une même fonction ont en commun. Soient F et G deux primitives d'une même fonction f sur un intervalle I. Comme F est une primitive de f alors F est dérivable sur I et F' = f.
Intéressons-nous à la fonction F - G. (F - G)'(x) = F'(x) - G'(x) = f(x) - f(x) = 0 Comme sa dérivée est nulle alors la fonction F - G est constante sur l'intervalle I.
Pour tout réel x de l'intervalle I, F(x) = G(x) + k.
|
Réciproquement, il est facile de démontrer que si F est une primitive de la fonction f alors la fonction
F + k est une autre primitive de f.
Ce qui nous donne en conclusion le théorème suivant ;
| Théorème : F est une primitive de la fonction f sur l'intervalle I.
Dire que G est une primitive de f sur I équivaut à dire qu' il existe une constante k tel que G = F + k. Deux primitives d'une même fonction diffèrent d'une constante k. |
Primitives des fonctions de référence.
Nous l'avons déjà dit : intégrer (ou "primitiver"), c'est la dérivation à l'envers.
Les primitives des fonctions de référence se déduisent donc des différentes formules de dérivation.
Note : pour montrer qu'une fonction F est une primitive de la fonction f, il suffit simplement de démontrer que la dérivée F' est égale à f.
Les fonctions sont classées en trois catégories :
Pour chaque cas, nous indiquerons l'intervalle sur lequel la primitive est valable.
Il s'agit d'ailleurs presque toujours de l'ensemble de définition de la fonction à intégrer...
| Fonctions puissances | |||
| Fonction | Primitive | Ensemble de définition | Annexe |
| 0 | k | ]- ; + ; + [ [ |
0 et 3 sont deux primitives de 0. |
| 1 | x + k | ]- ; + ; + [ [ |
Les primitives des fonction constantes sont les fonctions affines. |
| x |  |
]- ; + ; + [ [ |
|
| x2 | 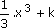 |
]- ; + ; + [ [ |
|
| x3 | 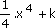 |
]- ; + ; + [ [ |
|
| xn | 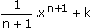 |
]- ; + ; + [ [ |
|
| Fonctions inverses et racine | |||
| Fonction | Primitive | Ensemble de définition | Annexe |
 |
ln(x) + k | ]0 ; + [ [ |
Aucune fonction n'a pour dérivée 1/x. La primitive de 1/x est une nouvelle fonction que l'on baptise logarithme. |
 |
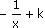 |
]- ; 0[ È ]0 ; + ; 0[ È ]0 ; + [ [ |
|
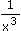 |
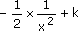 |
]- ; 0[ È ]0 ; + ; 0[ È ]0 ; + [ [ |
|
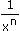 |
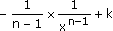 |
]- ; 0[ È ]0 ; + ; 0[ È ]0 ; + [ [ |
|
 |
 . x . . x .  + k + k |
[0 ; + [ [ |
Cette primitive est de la forme x1,5. La preuve |
 |
2. + k + k |
]0 ; + [ [ |
C'est la stricte conséquence de dérivée de la fonction racine. |
| Fonctions trigonométriques, logarithme et exponentielle | |||
| Fonction | Primitive | Ensemble de définition | Annexe |
| sin(x) | -cos(x) | ]- ; + ; + [ [ |
Quel... |
| cos(x) | sin(x) | ]- ; + ; + [ [ |
...couple ! |
| tan(x) | - ln(cos(x)) | ]- /2 ; /2 ;  /2[ /2[ |
La preuve |
| ln(x) | x . ln(x) - x | ]0 ; + [ [ |
La preuve |
| ex | ex | ]- ; + ; + [ [ |
Une histoire de dérivée... |
| xa | 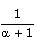 .xa+1 .xa+1 |
]0 ; + [ [ |
Une histoire de dérivée... |
| ax | 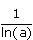 . ax . ax |
]- ; + ; + [ [ |
Une histoire de dérivée... |
| Nous ne l'avons pas mise mais pour être rigoureux, il faudrait rajouter à l'expression de chaque primitive : + constante k | |||
 D'autres primitives plus "exotiques".
D'autres primitives plus "exotiques".
Pour conclure cette page, nous allons aborder les primitives de fonctions
plus exotiques : les réciproques des trigonométriques. Elles sont toutes hors programme : voilà une bonne raison d'en parler
Voici donc les primitives des fonctions arcsinus, arccosinus, arctangente ainsi que certaines autres qui en dérivent...
| Fonctions trigonométriques réciproques et autres | |||
| Fonction | Primitive | Ensemble de définition | Annexe |
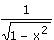 |
arcsin(x) | ]-1 ; 1[ | Autre expression de la primitive : /2 - arccos(x). /2 - arccos(x).Simple conséquence de la dérivation |
 |
arctan(x) | ]- ; + ; + [ [ |
Simple conséquence de la dérivation |
| arcsin(x) | x . arcsin(x) +  |
]-1 ; 1[ | La preuve |
| arccos(x) | x . arccos(x) -  |
]-1 ; 1[ | La preuve |
| arctan(x) | x . arctan(x) - |
]- ; + ; + [ [ |
La preuve |
| Nous ne l'avons pas mise mais pour être rigoureux, il faudrait rajouter à l'expression de chaque primitive : + constante k | |||