 |
Ce qui est développé dans cette page n'est à priori pas du programme de Terminale (même Scientifique). C'est d'ailleurs qu'il nous a semblé nécessaire d'en parler. Le tout repose sur une notion aujourd'hui délaissée bien qu'utile : l'intégration par parties. |
Primitives par parties
comment déterminer certaines primitives
Après avoir expliqué ce qu'est l'intégration par parties, nous nous attacherons à montrer comment il est possible en utilisant cette technique de déterminer les primitives des fonctions
racine, logarithme, arcsinus,
arccosinus et arctangente.
Les deux flèches 
 de la barre de sommaire vous permettront de remonter à la page précédente ou d'accéder à la suivante.
de la barre de sommaire vous permettront de remonter à la page précédente ou d'accéder à la suivante.
L'intégration par parties.
Vous l'aurez certainement remarqué mais l'intégration d'une fonction (c'est-à-dire le fait de lui trouver une primitive) est assez peu compatible avec le produit.
Cependant dans certains cas, il est possible de contourner le problème en procédant à une intégration par parties.
Soient u et v deux fonctions dérivables sur un intervalle I.
Comme elles sont dérivables sur I alors il en va de même pour leur produit. De plus :
| (u.v)' |
= |
u.v' + u'.v |
| d'où |
| u.v' |
= |
(u.v)' - u'.v |
Cette dernière égalité nous permet de connaître une primitive de u.v'. En effet, la différence passe magnifiquement le cap de l'intégration. Ainsi donc :
Primitive de u.v' = Primitive de (u.v)' - Primitive de u'.v
Or une primitive de la dérivée du produit u.v
est cette fonction u.v.
Finalement, on a donc l'égalité :
Primitive de u.v' = u.v - Primitive de u'.v
Autrement écrit, au lieu de chercher une primitive de u.v', il faut trouver une primitive de u'.v.
On pourrait croire que l'on a simplement déplacé le problème. Ce n'est parfois qu'une impression.
Illustration avec ce qui suit... |
Une primitive pour  .
.
Déterminons à l'aide d'une intégration par parties une primitive de la fonction racine.
Ce n'est pas une découverte mais pour tout réel strictement positif x, on peut écrire que :
 =
=  × 1
× 1
Nous allons intégrer par parties le produit  × 1.
× 1.
Les fonctions u et v sont définies alors par :
- u(x) =
 .
.
Cette fonction u est dérivable sur ]0 ; + [. De plus, u'(x) =
[. De plus, u'(x) =  ×
×  .
.
- v'(x) = 1.
La fonction v est par exemple : v(x) = x.
En vertu de ce que nous avons dit précédemment,
nous pouvons écrire que :
| Primitive de u.v' |
= |
u.v - Primitive de u'.v |
Primitive de  × 1 × 1 |
= |
 . x - Primitive de . x - Primitive de  × ×  . x . x |
Il ne reste plus alors qu'à simplifier l'écriture et à manoeuvrer :
Primitive de  |
= |
 . x - . x -  . Primitive de . Primitive de  |
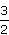 × Primitive de × Primitive de  |
= |
 . x . x |
Primitive de  |
= |
 . .  . x . x |
Reste à préciser ce qui sa passe en 0 car là nous avons supposé que x était strictement positif.
En fait, c'est un faux problème car la fonction  × x.
× x. est dérivable en 0 et son nombre dérivé y est 0.
est dérivable en 0 et son nombre dérivé y est 0.
Une primitive pour le logarithme népérien.
Déterminons à l'aide d'une intégration par parties une primitive de la fonction logarithme népérien.
Nous allons commencer notre raisonnement par une audacieuse astuce déjà utilisée avec la racine !
Pour tout réel strictement positif x, on peut écrire que :
ln(x) = ln(x) × 1
Comme nous allons user d'une intégration par parties ce produit, il nous faut définir les fonctions u et v.
- u(x) = ln(x).
Cette fonction u est dérivable sur ]0 ; + [. De plus, u'(x) =
[. De plus, u'(x) =  .
.
- v'(x) = 1.
La fonction v est par exemple : v(x) = x.
En vertu de ce que nous avons dit au début, nous pouvons écrire que :
| Primitive de u.v' |
= |
u.v - Primitive de u'.v |
| Primitive de ln(x) |
= |
ln(x) . x - Primitive de  . x . x |
|
= |
ln(x) . x - Primitive de 1 |
|
= |
ln(x) . x - x |
Conclusion : une primitive du logarithme népérien sur l'intervalle ]0 ; + [ est une fonction de la forme
: [ est une fonction de la forme
:
F(x) = x.ln(x) - x + k .
|
Une primitive pour Arcsinus.
Déterminons à l'aide d'une intégration par parties une primitive de arcsinus
sur l'intervalle ]-1 ; 1[.
La fonction arcsinus est définie sur l'intervalle [-1 ; 1] mais seulement dérivable sur ]-1 ; 1[.
Pour tout réel x de cet intervalle, on peut écrire que :
arcsin(x) = arcsin(x) × 1
Les deux fonctions u et v requises pour une intégration par parties sont donc définies par :
- u(x) = arcsin(x).
u est dérivable sur [-1 ; 1] et u'(x) =  .
.
- v'(x) = 1.
La fonction v est par exemple : v(x) = x.
En vertu de ce que nous avons dit au début, nous pouvons écrire que :
| Primitive de u.v' |
= |
u.v - Primitive de
u'.v |
| Primitive de arcsin(x) |
= |
arcsin(x) . x - Primitive de  . x
. x |
Or la fonction x .  est une fonction de la forme g'(x) . f'(g(x)) où :
est une fonction de la forme g'(x) . f'(g(x)) où :
- g(x) = x2 donc g'(x) = 2.x.
- f(t) =
 donc f'(t) =
donc f'(t) =  .
.
Une primitive de x .  est donc -
est donc - . Ainsi donc :
. Ainsi donc :
Primitive de arcsin(x) = arcsin(x) . x + 
| Conclusion : une primitive de arcsinus sur l'intervalle ]-1 ; 1[ est une fonction de la forme :
F(x) = x . arcsin(x) +  + k . + k .
|
Note : certains objecterons (à raison) qu'une telle primitive est aussi définie en -1 et en 1. C'est vrai !
En fait, F est bel et bien une primitive d'arcsinus sur tout l'intervalle mais ça, je ne suis pas encore arrivé à le démontrer... Si jamais, vous aviez la solution de cette énigme, contactez-moi. |
Une primitive pour Arccosinus.
Déterminons à l'aide d'une intégration par parties une primitive de arccosinus
sur l'intervalle ]-1 ; 1[.
Notre raisonnement va reprendre en grande partie ce qui a été fait pour arcsinus.
A l'instar de la fonction arcsinus, arccosinus est définie sur l'intervalle [-1 ; 1] mais n'est dérivable que sur ]-1 ; 1[.
Pour tout réel x de cet intervalle, on peut écrire que :
arccos(x) = arccos(x) × 1
Les deux fonctions u et v d' une intégration par parties sont alors définies par :
- u(x) = arccos(x).
u est dérivable sur [-1 ; 1] et u'(x) = - .
.
- v'(x) = 1.
La fonction v est par exemple : v(x) = x.
En vertu de ce que nous avons dit au début, nous pouvons écrire que :
| Primitive de u.v' |
= |
u.v - Primitive de u'.v |
| Primitive de arccos(x) |
= |
arccos(x) . x - Primitive de  - -  . x . x |
Or nous avons vu avec arcsinus qu'une primitive de - x .  est
est  . Ainsi donc :
. Ainsi donc :
Primitive de arccos(x) = arccos(x) . x - 
| Conclusion : une primitive de arccosinus sur l'intervalle ]-1 ; 1[ est une fonction de la forme :
F(x) = x . arccos(x) -  + k . + k .
|
Note : à l'instar de la primitive d'arcsinus, F n'est pas seulement la primitive d'arccosinus sur ]-1 ; 1[. Elle l'est en fait sur tout l'intervalle [-1 ; 1].
Seul problème : comment démontre-t-on que F est dérivable en -1 et en 1 ? Si jamais, vous aviez la solution de cette énigme, contactez-moi. |
Une primitive pour Arctangente.
Déterminons à l'aide d'une intégration par parties une primitive de arctangente sur ]- ; +
; + [.
[.
La fonction arctangente est définie et dérivable sur ]- ; +
; + [.
[.
Comme pour toutes les autres, on peut écrire que pour tout réel x :
arctan(x) = arctan(x) × 1
Les deux fonctions u et v d' une intégration par parties sont alors définies par :
- u(x) = arctan(x).
u est dérivable sur ]- ; +
; + [ et u'(x) =
[ et u'(x) =  .
.
- v'(x) = 1.
La fonction v est par exemple : v(x) = x.
En vertu de ce que nous avons dit au début, nous pouvons écrire que :
| Primitive de u.v' |
= |
u.v - Primitive de u'.v |
| Primitive de arctan(x) |
= |
arctan(x) . x - Primitive de  . x . x |
Or la fonction x .  est presque une fonction de la forme g'(x) . f'(g(x)) où :
est presque une fonction de la forme g'(x) . f'(g(x)) où :
- g(x) = x2 donc g'(x) = 2.x.
- f(t) = ln(1 + t) donc f'(t) =
 .
.
Une primitive de x .  est donc
est donc  . ln(1 + x2). Ainsi :
. ln(1 + x2). Ainsi :
Primitive de arctan(x)& = x . arctan(x) -  . ln(1 + x2)
. ln(1 + x2)
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par
la taverne de l'Irlandais.
(c) AMLTI Juillet 2000/Janvier 2003. Tous droits réservés.


 de la barre de sommaire vous permettront de remonter à la page précédente ou d'accéder à la suivante.
de la barre de sommaire vous permettront de remonter à la page précédente ou d'accéder à la suivante. .
. =
=  [. De plus, u'(x) =
[. De plus, u'(x) =  ×
×  .
.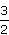 × Primitive de
× Primitive de  .
.  .
. .
. donc f'(t) =
donc f'(t) =  .
.
 -
- . x
. x .
. .
.