Primitive de la fonction tangente

On sait que pour tout x de l'intervalle ]-/2 ; /2[, on a :   tan(x) = .

Or    est à un signe près une fonction de la forme g'(x) . f'(g(x)) où :

• g(x) = cos(x)  donc  g'(x) = -sin(x).
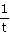• f'(t) =   donc  f(t) = ln(t).

Une primitive de    est donc  - ln(cos(x)).

Conclusion : une primitive de tangente sur l'intervalle ]-/2 ; /2[ est une fonction de la forme : F(x) = - ln(cos(x)) + k

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Juillet 2000/Janvier 2003. Tous droits réservés.