Les fonctions trigonométriques demeurent l'exclusivité des sections scientifiques. Les plupart des formules qui seront démontrées dans cette page sont abordées en Première Scientifique. D'autres sont hors de tout programme. Voilà, pourquoi nous en parlerons...

Un mot d'introduction.
Les fonctions trigonométriques sont à notre époque de veilles connaissances de Seconde. Malgré tout ce qui a été fait, nous ne connaissons pas grand chose sur celles-ci. Ce chapitre va nous donner l'occasion d'aller plus loin, d'en apprendre plus sur les propriétés des sinus, cosinus et autres tangentes.
Car si ces dernières ne laissent pas passer des sommes, des différences ou des produits, elles n'en font pas pour autant n'importe quoi. Ce sont ces histoires que nous allons vous raconter.

Outre cette présente page, Trigonométrie : Formules 1  comporte un formulaire récapitulant toutes les formules abordées ainsi qu'un module d'apprentissage.
Bref tout pour aller plus loin et surtout à partir d'ailleurs...

Cosinus, sinus et tangente d'une somme ou d'une différence.
Toutes les formules que nous allons établir repose sur une seule d'entre elles. Elle constituera le pierre angulaire de notre offensive. C'est d'elle que d'où découlera et c'est par elle que nous commenceront.

	Cosinus d'une différence : le fondement. Soient a et b deux nombres réels quelconques. Notre mission est d'exprimer  cos(a - b)  en fonction des cosinus et sinus de a et de b. Pour la remplir, nous allons nous appuyer sur le produit scalaire de deux vecteurs dans le plan... Plaçons-nous dans un repère orthornomé direct. On appelle A le point du cercle trigonométrique associé au réel a. L'angle orienté ( , ) fait donc a radians. De plus, le point A a pour coordonnées (cos(a) ; sin(a)). On appelle B le point du cercle trigonométrique associé au réel b. ( , ) mesure donc b radians. De plus, B(cos(b) ; sin(b)) Tout est à présent en place pour la bataille... Le produit scalaire  ·   peut être vu de deux manières : De manière classique. On a alors que : · = × × cos( , ) = 1 × 1 × cos(b - a) = cos(a - b) Car le cosinus d'angle et celui de son opposé sont égaux...    De manière analytique. On peut alors écrire que : · = xA . xB + yA . yB = cos(a) . cos(b) + sin(a) . sin(b) Ainsi en conclusion : cos(a - b) = · = cos(a) . cos(b) + sin(a) . sin(b)  Nous avons donc une première formule. En fait, nous en avons deux ! En effet : cos(a + b) = cos(a - (-b)) = cos(a) . cos(-b) + sin(a) . sin(-b) = cos(a) . cos(b) - sin(a) . sin(b) La mission est donc accomplie au-delà de toute espérance. Nous pouvons donc conclure ! Conclusion : Si a et b sont deux réels alors : cos(a + b) = cos(a) . cos(b) - sin(a) . sin(b) cos(a - b) = cos(a) . cos(b) + sin(a) . sin(b)

Après nous être occupé du cosinus, il nous est désormais possible de nous prononcer sur les sinus et tangentes d'une somme ou d'une différence. Ainsi :

• Pour le sinus.

  Pour ce qui est de la somme.

  

  A partir de la somme, on peut alors s'attaquer au sinus de la différence.

  sin(a - b) = sin(a + (-b))	= sin(a) . cos(-b) + cos(a) . sin(-b)
  	= sin(a) . cos(b) - cos(a) . sin(b)

   

  Conclusion : Si a et b sont deux réels alors :     sin(a + b) = sin(a) . cos(b) + cos(a) . sin(b)     sin(a - b) = sin(a) . cos(b) - cos(a) . sin(b)

   
• Pour la tangente.

  Pour ce qui est de la somme.

   
  

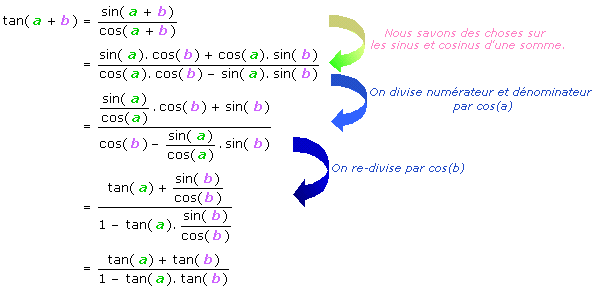
  Sachant que la tangente est une fonction impaire, la différence n'est plus alors qu'une affaire de moins.

   
  

  Conclusion : Si a et b sont deux réels différents de  /2 +k.  et dont la somme (ou la différence) ne l'est pas non plus alors :     tan(a + b) =     tan(a - b) =

A partir de ces trois doublettes de formules, on en établit d'autres concernant le double d'un angle. Ainsi :

cos(2.a) = [cos(a)]2 - [sin(a)]2 = 2 . [cos(a)]2 - 1 = 1 - 2 . [sin(a)]2 =

sin(2.a) = 2. cos(a) . sin(a) =

tan(2.a) =

Somme, différence, produit de cosinus, sinus ou tangentes... et réciproquement !
Le but du jeu est d'exprimer un produit de sinus ou de cosinus de manière plus simple.
Pour remplir cette impossible nouvelle mission, nous n'aurons pas à chercher bien loin. Nous allons simplement nous servir de ce que nous avons fait au premier paragraphe.
Dans ce qui suit, a et b seront toujours deux réels quelconques.

• Simplifier un produit de cosinus :  cos(a) . cos(b).
  Peut-être cela vous a-t-il échappé, mais à un certain moment nous avons démontré que :
  

  cos(a + b) = cos(a) . cos(b) - sin(a) . sin(b)		cos(a) . cos(b) = cos(a + b) + sin(a) . sin(b)
  cos(a - b) = cos(a) . cos(b) + sin(a) . sin(b)		cos(a) . cos(b) = cos(a - b) - sin(a) . sin(b)
  		2 . cos(a) . cos(b) = cos(a + b) + cos(a - b)

  Ainsi on peut conclure que :

  Conclusion : si a et b sont deux réels quelconques alors :

   

  Et puis, on peut essayer voir les choses à l'envers. Autrement écrit, on peut chercher à exprimer une somme de cosinus à partir d'un produit...
  p et q étant deux réels quelconques, à quoi est donc égal cos(p) + cos(q) ?

  Et utilisant la formule précédente, il s'agit donc de trouver deux réels a et b tels que :

  2 . cos(a) . cos(b) = cos(a + b) + cos(a - b) = cos(p) + cos(q)

  Autrement dit :

  a + b = p     et     a - b = q

  A l'issue d'interminables calculs, on arrive à :

  a =        et      b =

  On en déduit alors la formule recherchée.

  Conclusion : si p et q sont deux réels quelconques alors :

   
    
• Simplifier un produit de sinus :  sin(a) . sin(b).
  A un certain moment de notre aventure, nous avons établi que :
  

  cos(a + b) = cos(a) . cos(b) - sin(a) . sin(b)		sin(a) . sin(b) = cos(a) . cos(b) - cos(a + b)
  cos(a - b) = cos(a) . cos(b) + sin(a) . sin(b)		sin(a) . sin(b) = cos(a - b) - cos(a) . cos(b)
  		2 . sin(a) . sin(b) = cos(a - b) - cos(a + b)

  Ainsi on peut conclure que :

  Conclusion : si a et b sont deux réels quelconques alors :

  Comme précédemment, on peut essayer de regarder la formule à l'envers. Autrement écrit, on peut chercher à quoi est égal une différence de cosinus.
  La manière de procéder est à peu prés la même ! A l'issue d'infinissables calculs, on arrive à :

  Conclusion : si p et q sont deux réels quelconques alors :

    
    
• Simplifier un produit mixte sinus/cosinus :  sin(a) . cos(b).
  Le premier paragraphe fut l'instant où nous vîmes que :
  

  sin(a + b) = sin(a) . cos(b) + cos(a) . sin(b)		sin(a) . cos(b) = sin(a + b) - cos(a) . sin(b)
  sin(a - b) = sin(a) . cos(b) - cos(a) . sin(b)		sin(a) . cos(b) = sin(a - b) + cos(a) . sin(b)
  		2 . sin(a) . cos(b) = sin(a + b) + sin(a - b)

  Ainsi on peut conclure que :

  Conclusion : si a et b sont deux réels quelconques alors :

   

  Et puis, comme pour les deux cas d'avant, on peut essayer de voir cette formule dans l'autre sens. On s'intéresse alors à la somme de deux sinus.
  La démarche est la même donc nous laisserons les inachevables calculs à notre vénéré lecteur !

  Et puis à partir de la formule obtenue pour la somme, sachant que  sin(p) - sin(q) = sin(p) + sin(-q), on en déduit alors une autre sur la différence de deux sinus.

  Conclusion : si p et q sont deux réels quelconques alors :

Dans ce que nous venons de faire, nous avons parlé de sommes et de différences de cosinus ou de sinus, mais nous n'avons rien de la tangente. Nous allons réparer cet oubli sur le champ !

Soient donc  p et q deux réels non congrus à /2 modulo , c'est-à-dire deux réels pour lesquels la tangente existe !
On peut alors écrire que :

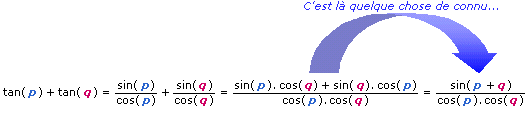
Nous venons d'établir deux formules : une pour la somme de deux tangentes et une autre pour la différence car la tangente est une fonction impaire.

Conclusion : si p et q sont deux réels non congrus à /2 modulo alors :

Ces dernières formules avec celles qui les ont précédées constituent une bibliothèque sur laquelle il sera possible de s'appuyer pour établir de nouveaux énoncés, pour aller plus loin, bien au-delà de la Seconde ou de la simple trigonmétrie....

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Février 2001/Janvier 2003. Tous droits réservés.