Du côté de Z...

Cette page aborde et approfondit des notions effleurées en Troisième. En principe, elle s'adresse aux élèves de Terminale Scientifique spécialité maths. Elle s'appuie sur la page Juste au-delà de Z. A son exemple, elle va parfois un peu plus loin que ce qui est nécessaire pour le BAC....
Pour en savoir plus sur certains sujets, cliquer votre curseur sur le logo . Pour refermer la fenêtre, il vous suffira de recliquer sur le logo.

Après avoir regardé ce qu'il y avait juste au-delà de Z, nous allons aborder au travers de cet anneau deux notions importantes.
La première s'appelle PGCD. Elle conduit aux nombres premiers entre eux, au théorème de Bezout et à celui de Gauss.
La seconde se nomme PPCM. Elle complète la première.
Ces deux notions abordées en Terminale Scientifique ne sont pas spécifiques à l'anneau . Leurs études sur cet ensemble préfigurent ce qu'elles sont ailleurs. Voilà pourquoi nous allons regardé du côté de .

Du côté des diviseurs communs : le PGCD.
PGCD est l'acronyme de Plus Grand Commun Diviseur.
Cette notation n'est pas en elle-même une nouveauté. En effet, la notion a été introduite en Troisième. Mais elle l'était alors pour les entiers naturels. Nous allons l'étendre à tous les entiers qu'ils soient négatifs ou positifs.

Pour avoir des choses en commun, il faut au moins être deux : c'est là la base du partage.
Prenons par exemple deux entiers positifs comme 36 et 48. Dressons les listes de leurs diviseurs respectifs.

Ceux de 36	1 2 3 4 6 9 12 18 36
Ceux de 48	1 2 3 4 6 8 12 16 24 48

Le plus grand de leurs diviseurs communs est clairement 12. On écrit alors que :

PGCD(36 ; 48) = 12

En fait, nous n'avons que des diviseurs positifs, ceux dans . Seulement nous avons pour vocation à travailler dans .
Si 9 est un diviseur de 36, il en va de même pour -9. En effet, on a bien que :

36 = (-9) × (-4) Dans

, les listes des diviseurs de 36 et 48 sont donc :

Ceux de 36	-1 -2 -3 -4 -6 -9 -12 -18 -36 1 2 3 4 6 9 12 18 36
Ceux de 48	-1 -2 -3 -4 -6 -8 -12 -16 -24 -48 1 2 3 4 6 8 12 16 24 48

Une question se pose alors : c'est quoi alors le PGCD de 36 et 48 dans ?
Car si 12 peut clairement prétendre à cette distinction, on ne voit pas pourquoi il n'en irait pas de même pour son opposé -12.
Cela nous fait donc deux PGCD en puissance ! Il nous faut donc donner une nouvelle définition de la notion de PGCD !

Intéressons-nous à l'ensemble des diviseurs communs de 36 et 48.

Diviseur(36 ; 48) = {-12 ; -6 ; -4 ; -3 ; -2 ; -1 ; 1 ; 2 ; 3 ; 4 ; 6 ; 12}

Une chose que saute aux yeux avec plus ou moins de rapidité est que n'importe lequel de ces entiers divise -12 et 12. Nous tenons là le source de cette nouvelle définition...

Définition (la vraie) du Plus Grand Commun Commun :
Dire que le nombre d est un Plus Grand Diviseur Commun des nombres a et b signifie que :

d divise a et b.
Si c est un diviseur commun de a et de b alors c divise d.

Remarque : Lorsque nous parlons de nombres, nous entendons entiers relatifs car nous travaillons dans l'anneau . Cependant cette définition du PGCD est valable dans n'importe quel anneau...

Avec cette définition, -12 et 12 peuvent prétendre au titre de PGCD de 36 et 48 ! En effet, n'importe lequel des diviseurs communs de ces derniers (que ce soit -6, 3 ou 4) divisent -12 et 12.

Une chose évidente est que les diviseurs dans de 36 aussi sont ceux de -36.
Donc nous pouvons affirmer que les PGCD des couples (-36 ; 48), (36 ; -48) et (-36 ; -48) sont aussi -12 et 12.

De manière générale, les PGCD de deux entiers relatifs (quelque soient leurs signes) sont ceux de leurs valeurs absolues.
Ainsi au lieu de rechercher les PGCD de -456 et -678, s'intéressera-t-on plutôt à ceux de 456 et 678.

Le truc en plus : le PGCD de deux entiers relatifs existe-t-il toujours ?
Voilà une question que nous avons omis de traiter. En effet, rien ne garantit deux entiers aient toujours un PGCD sinon notre bonne parole.
Si l'existence d'un plus grand élément dans l'ensemble des diviseurs communs ne fait pas de doute, en revanche rien ne garantit qu'il vérifiera la condition 2 de la définition : tout diviseur commun c le divisera-t-il ?
Cependant, malgré ce doute, la réponse est cette question est oui

.

La seconde condition de notre définition fait que deux PGCD d'un même couple (a ; b) se divisent nécessairement mutuellement. On dit alors qu'ils sont associés.
Or être associés dans signifie être égaux ou opposés...
Dans

à l'instar de 36 et 48, deux entiers non nuls ont en tout en pour tout deux PGCD : l'un est l'opposé de l'autre.

Nous allons prouver que le PGCD de deux nombres existe toujours...
Notre action ne concernera que les entiers naturels. En effet, si nous établissons l'existence pour eux alors il en ira de même pour tous les entiers de

. Ceci car les diviseurs de -36 sont aussi ceux de 36...

a et b sont deux entiers positifs. On appelle Div(a ;b) l'ensemble de leurs diviseurs communs dans .
Comme 1 en fait partie, il est clair que Div(a ; b) n'est pas vide.
De plus, il est clair que tout diviseur de a et de b est plus petit ou égal à ces deux-là.
Donc Div(a ; b) a un plus grand élément. Appelons-le d.
Il est clair que d est un entier naturel. En effet, n'oublions pas que 1 fait partie de Div(a ; b).
Comme d est le plus grand diviseur commun à a et b, il existe donc deux entiers strictement positifs k et k' tels que :

a = k . d et b = k' . d

Il nous reste à prouver que ce d vérifie la condition 2 de la définition...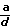
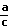Prenons c un diviseur positif commun de a et de b différent de d.
Comme il divise ces deux là, les restes des divisions de c par a ou par b sont égaux à 0.
Effectuons la division euclidienne de d par c. Il existe donc deux entiers naturels q et r tels que :

d = q . c + r avec r < c.Multiplions cette égalité par k. Il vient alors que : a = (k .q) . c + k . r Seulement comme c < d alors k =

. Par conséquent, k . r est donc strictement plus petit que a.
k.r est donc le reste de la divisions euclidienne de a par c.
Or nous savons que ce reste est nul. Comme k est un entier strictement positif, c'est donc que r est égal à 0.

Comme le reste r de la division euclidienne de d par c est nul, c'est donc que tout diviseur positif c divise d.
De plus, il en va de même pour tous les diviseurs négatifs -c...

Pour conclure ce débarquement algébrique, nous allons définir ce que sont deux (et même plus) nombres premiers entre eux.

Définition de la priméralité de deux nombres entre eux.
Dire que deux nombres sont premiers entre eux (ou étangers) signifie qu' un de leur PGCD est 1.

Par exemple, -55 et 24 sont premiers entre eux car un de leur plus grand diviseur commun est 1.

De manière générale, deux entiers relatifs sont premiers entre eux si leurs deux PGCD sont -1 et 1.

Les chemins de théorème Bezout.
Le théorème de Bezout est un énoncé permettant de caractériser deux nombres premiers entre eux sans pour calculer leur PGCD.
Certains voudraient vous faire croire que ce n'est que cela. Sauf que la vérité ne s'arrête pas à ce théorème mais qu'elle y commence. Voici donc l'histoire vraie de ce théorème.

A l'origine du théorème, il y a l'identité éponyme.

Proposition : (identité de Bezout).
Si d est un PGCD des nombres a et b alors il existe deux nombres u et v tels que a.u + b.v = d.

Là encore, précisons que par "nombre" nous entendons entier relatif ! Mais cet énoncé est transposable dans bien d'autres anneaux principaux...
L'identité de Bezout a une histoire et une démonstration.

La preuve de l'identité de Bezout
On appelle I l'ensemble des entiers naturels de la forme a.n + b.m où n et m sont deux entiers relatifs.
Nous allons démontrer que le PGCD D fait partie de cet ensemble.

La première chose à dire est que I est non vide. En effet 0, a et b en font partie.
Comme tout sous-ensemble de , I admet donc un plus petit élément non nul. Appelons-le p.

p appartenant à I, il existe deux entiers naturels u et v tels que :

p = a.u + b.v

Comme tout élément de I, p est clairement divisible par les diviseurs communs à a et b. Il l'est donc en particulier pour le plus grand d'entre eux qu'est leur PGCD D.
Ainsi D divise p ! Une conséquence de ceci est que D p.

Il reste à prouver qu'il s'agit d'une égalité. La dernière étape va consister à démontrer que p est un diviseur commun à a et b

Effectuons la division euclidienne a de p. Il existe donc un seul couple d'entiers naturels (q ; r) tels que :

a = q . p + r avec 0

r < p On peut alors écrire que :

r = a - q . p = a - q . (a.u + b.v) = a . (1 - q.u) + b . v

r est donc un élément de l'ensemble I qui est strictement plus petit que p.
Compte tenu de ce qu'est p, r est donc nécessairement égal à 0.
Le reste de la division euclidienne étant nul, p est donc un diviseur de a.

De la même façon, on montre que p est un diviseur de b.
En récapitulant, nous savons que p est un diviseur commun à a et b et aussi que p est supérieur ou égal à leur Plus Grand Commun Diviseur D. Donc les entiers naturels p et D sont nécessairement égaux.
Le PGCD de a et b est donc bien de la forme a.u + b.u

Ainsi il existe deux entiers u et v (peut-être plus ?) tels que 36.u + 48.v = 12 !

Le truc en plus : la réciproque de cette proposition est fausse !
Cette proposition n'est vraie que dans un seul sens ! Toute égalité de la forme a.u + b.v = d ne fait pas nécessairement de d un PGCD de a et de b !
C'est cependant le cas si d est un diviseur de a et b ! Car seuls les plus grands de leur diviseurs communs peuvent vérifier ce genre d'égalité !

C'est à partir de l'identité de Bezout que l'on démontre ce si important théorème éponyme.

Théorème de Bezout.
Dire que les nombres a et b sont premiers entre eux équivaut à dire qu' il existe deux nombres
u et v tels que a.u + b.v = 1.

La preuve de ce théorème.

Nous avons deux choses à démontrer. La première est que si deux nombres sont premiers alors on a l'égalité. La seconde est que si on a l'égalité alors on a des nombres premiers entre eux. Au boulot !

Supposons que a et b soient premiers entre eux. Cela veut donc dire que leur PGCD est 1.
En application de l'identité de Bezout, il existe donc deux entiers u et v tels que a.u + b.v = 1.
a et b sont deux entiers. Supposons qu'il existe deux nombres u et v tels que a.u + b.v = 1.
Prenons c un diviseur commun à a et b.
Il est clair que c divise la somme a.u + b.v c'est-à-dire 1.
Or quels sont les diviseurs de 1 ? Il n'y en a que deux : ce sont -1 et 1.
Cela signifie clairement que les entiers relatifs a et b sont premiers entre eux !

D'où le théorème !

On pourrait croire que le théorème de Bezout ne sert à rien. C'est en partie faux ! En voici quelques exemples d'application.

Pourquoi deux nombres consécutifs sont-ils nécessairement premiers ?
Prenons deux entiers relatifs non nuls consécutifs n et n+1.
Il est peu glorieux d'écrire que (n+1) + (-1) × n = 1.
Pourtant, cela et Bezout permettent de conclure que les entiers n et n+1 sont premiers entre eux !
L'équation 4.x + 7.y = 1 admet-elle des solutions (x ; y) entières ?
Là encore, le théorème de Bezout va nous permettre de répondre que oui. En effet, comme 4 et 7 sont premiers entre eux alors il existe deux entiers relatifs u et v tels que 4.x + 7.v = 1.
En fait ici l'identité de Bezout qui joue ! Ici comme avec l'équation 6.x + 4.y = 2...
Par contre, l'équation 6.x + 4.y = 1 n'a pas de solutions entières car 6 et 4 ne sont pas premiers...

Une des conséquences fondamentales du théorème de Bezout est le théorème de Gauss qu'il sert à démontrer.

Théorème(Lemme) de Gauss.
a, b et c sont trois nombres (des entiers relatifs).

Si c divise le produit a.b et si c est premier avec a alors c divise nécessairement b.

La preuve de ce théorème.

La démonstration de ce si fondamental théorème sera un court sprint hyper-rapide ! Attention donc au départ !

La première chose à exploiter est que comme c divise le produit a.b alors il existe un entier k tel que a.b = c.k

Ensuite, comme c et a sont premiers entre eux, c'est donc qu'il existe deux entiers u et v tels que a.u + c.v = 1.
Multiplions cette égalité par b. Il vient que :

b = a.b.u + c.b.v = c.k.u + c.b.v = c . (k.u + b.v)

Donc c divise b ! D'où le théorème de Gauss !

Gaussons-nous un peu !
Par exemple si 14 divise le produit 3.n, pouvons-nous dire que 14 divise nécessairement n !
En effet, 14 et 3 sont premiers sont premiers entre eux et il y a Gauss !

Des propriétés pour le PGCD.
Le théorème et l'identité de Bezout que nous venons de démontrer sont à l'origine de deux propriétés intéressantes. Les voici.

Propriétés : a et b sont deux entiers relatifs.

Pour tout entier k, PGCD(k.a ; k.b) = k . PGCD(a ; b).
Si r est le reste de la division euclidienne de a par b alors PGCD(a ; b) = PGCD(b ; r)

La preuve de ces deux propriétés.

Une chose que nous utiliserons pour les deux propriétés : quant on divise tous les termes d'une somme ou d'une différence, on divise celles-ci.

On appelle d un PGCD de a et b. Nous allons montrer que k.d est un PGCD de k.a et k.b.
La première chose à remarquer est que k.d est un diviseur commun de k.a et k.b.
Nous allons à présent montrer que n'importe lequel des diviseurs communs à k.a et k.b. le divise !
Soit c un diviseur commun à k.a et k.b.
Comme d est le PGCD de a et b, il existe donc d'après Bezout deux entiers u et v tels que a.u + b.v = d.
Multiplions cette égalité par k. Il vient alors que : (k.a).u + (k.b).v = k.d.c divisant k.a et k.b, il divise donc la somme qu'est k.d.
Cela fait de k.d un PGCD de k.a et k.b.
D'où la première propriété...
Pour parvenir à nos fins, nous allons démontrer que les diviseurs du premier couple sont ceux du second et réciproquement !
Comme r est le reste de la division euclidienne de a par b alors il existe un entier q tel que a = b.q +r.
Cette égalité s'écrit aussi : r = a - b.q
Soit c est un diviseur commun à a et b. De part la précédente égalité, il est clair que c divise aussi r.
Les diviseurs communs à a et b sont donc aussi ceux communs à b et r.
De même comme a = b.q + r, on montre que les diviseurs communs à b et r sont aussi ceux communs à a et b.

En conclusion, les couples (a ; b) et (b ; r) ayant les mêmes diviseurs communs, ils ont donc les mêmes PGCD. D'où la propriété.

Une conséquence de la propriété 1 : si a divise b alors un PGCD de ces deux entiers est a.
Cette conséquence peut paraître naturelle, il nous faut cependant la prouver.

Comme a divise b alors il existe un entier naturel q tel que b = a.q. On peut alors écrire que :

PGCD(a ; b) = PGCD(a×1 ; a×q) = a × PGCD(1 ; q) = a × 1 = a

On pourrait croire ces deux propriétés sans utilité. Il n'en est rien car elles permettent l'élaboration de méthodes de calculs pour le PGCD.

Pour déterminer le PGCD de deux nombres, il existe globalement quatre méthodes :

Lister tous les diviseurs communs.
Cette méthode, nous l'avons déjà utilisée dans le premier paragraphe avec 36 et 48.
Plus les entiers sont grands et plus elle perd en efficacité.
Utiliser la décomposition en facteurs premiers.
Nous le savons : tout entier relatif est décomposable en un produit de facteurs premiers. Connaissant les décompositions des deux entiers initiaux, il est possible de reconstituer leur PGCD. Tout repose sur le théorème suivant :

Théorème : (p_i)_i{1...n} est une famille d'entiers relatifs premiers non associés.

Prenons par exemple encore -36 et 48. Décomposons-les en facteurs premiers. On peut donc écrire que :

-36 = (-1) × 2² × 3² et 48 = 2⁴ × 3

Un PGCD de -36 et 48 est donc 2^inf(2;4) × 3^inf(2;1) = 2² × 3¹ = 12

Pour qu'élégante que soit cette méthode, elle requiert tout de même la décomposition des deux entiers en deux produits de facteurs premiers. Un travail qui est tout de même peu rentable au regard de ce qu'est un PGCD.
Le théorème ci-dessous se démontre plus ou moins simplement avec l'aide du théorème de Gauss et du principe "Combien puis-je caser de chaque p_i dans a et dans b ?"

Utiliser l'algorithme d'Euclide.
L'algorithme d'Euclide consiste en une suite de divisions euclidiennes successives. Il repose sur la propriété 2.

En lui-même, l'algorithme d'Euclide n'est pas une nouveauté puisqu'il a déjà été vu en Troisième. On peut le résumer par le diagramme suivant :

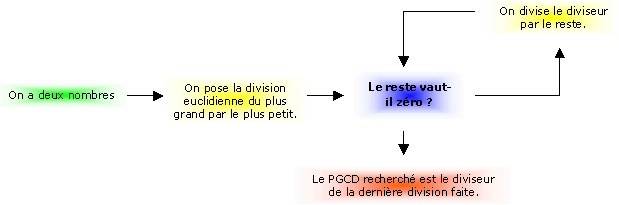
Tel qu'il a été vu en Troisième, l'algorithme d'Euclide ne concerne que les entiers naturels. En fait en utilisant ce qui a été fait pour l'extension de la division euclidienne sur , il est possible de l'étendre à n'importe quels entiers relatifs.

C'est notre propriété 2 qui légitime l'algorithme d'Euclide : PGCD(a ; b) = PGCD(b ; reste de a par b).
Toute l'astuce de cet algorithme consiste à construire une suite décroissante de restes positifs r_n selon la méthode suivante :

Opérations		Reste	Commentaires
On divise a par b		r₀	(a ; b) et (b ; r₀) ont le même PGCD. 0 r₀ < \|b\|
On divise b par r₀		r₁	(b ; r₀) et (r₀ ; r₁) ont le même PGCD. 0 < r₁ < r₀
On divise r₀ par r₁		r₂	(r₀ ; r₁) et (r₁ ; r₂) ont le même PGCD. 0 r₂ < r₁
...	...	...	...
On divise r_n-1 par r_n		r_n+1	(r_n-1 ; r_n) et (r_n ; r_n+1) ont le même PGCD. 0 < r_n+1 < r_n
....	...	...	...

La première chose à dire est que les couples (a ; b), (b ; r₀), et tous les couples (r_n ; r_n+1) ont les mêmes PGCD.
Ensuite, plusieurs questions surgissent de cette cascade de divisions euclidiennes :

La première est : a-t-elle une fin ou continue-t-elle ad vitam eternam ?
La réponse à cette question est simple. Cette cascade constitue une suite strictement décroissante de restes qui sont avant tout des entiers naturels.
Il existe donc un rang p pour lequel r_p = 0.
Après p, le processus s'arrête car la division euclidienne par 0 n'existe pas !

La seconde est : comment trouve-t-on alors un PGCD de a et b ?
En supposant que le processus s'arrête au rang p, un PGCD de a et b est alors r_p-1.
Mais pourquoi en est-il ainsi ?
De part la dernière division euclidienne, nous savons que : r_p-2 = q . r_p-1 + 0.
Donc r_p-1 divise r_p-2.
En conséquence, un PGCD de ces deux entiers est donc r_p-1.
En remontant la cascade, il vient donc que un PGCD de a et b est r_p-1.

Voilà donc ce qu'est l'algorithme d'Euclide et pourquoi il marche !

La recherche de facteurs communs.
Une des utilisations de la première propriété est la détermination d'un PGCD par la recherche de facteurs communs. C'est un peu abstrait aussi donnons un exemple avec 56 et 84.

PGCD(56 ; 84)	= PGCD(4×14 ; 4×21)	car 56 et 84 sont divisibles par 4.
	= 4 × PGCD(7×2 ; 7×3)	car 14 et 21 sont dans la table de 7
	= 28 × PGCD(2 ; 3)	2 et 3 sont premiers entre eux...
	= 28 × 1 = 28

Cette méthode est efficace à condition de connaître ses tables et quelques tests de divisibilités comme ceux par 2, 3, 5 et 9...

Il existe certainement d'autres méthodes plus ou moins exotiques permettant de déterminer un PGCD. Si vous en connaissez, contactez-nous s'il vous plaît !

Du côté des multiples communs : le PPCM.
Une autre notion mythique de l'arithmétique est le Plus Petit Commun Multiple. C'est quelque part l'alter -ego du PGCD. D'ailleurs, nous le verrons : les deux notions sont plus liées qu'on ne le pense !

La notion de PPCM est quelque chose d'assez naturel dans .
Prenons par exemple notre couple vedette : 36 et 48. Pour connaître leur PPCM, il faut auparavant déterminer leurs multiples communs. Pas tous évidemment car il y en a une éternité mais au moins les premiers d'entre eux.
Pour obtenir les multiples communs à 36 et 48, il nous faut dresser les tables de ces deux entiers.

Multiples de 36	36 72 108 144 180 216 252 288 324 360 ....
Multiples de 48	48 96 144 192 240 288 336 384 432 480 ....

Leur Plus Petit Commun Multiple est clairement 144.

Remarque ou pinaillage : certains esprits mesquins pourraient objecter que le Plus Petit Multiple Commun à 36 et 48 est 0.
Dans l'absolu il est vrai que 0 est un multiple commun et qu'il est plus petit que 144. Mais quel serait alors l'intérêt de cette notion de PPCM ?
Ce paragraphe n'aurait plus de raison d'être car il serait égal à 0 pour tous les couples d'entiers. C'est pour cela que lorsque l'on parle de PPCM, l'on entend multiple commun strictement positif.

Nous avons donc trouvé le PPCM de 36 et 48 dans . Mais qu'en est-il dans l'anneau ?
Car dans cet ensemble, les multiples de 36 et 48 sont plus nombreux. Enumérons-les plus simples. Il y a donc :

Multiples de 36	-36 -72 -108 -144 -180 -216 -252 -288 -324 -360 .... 36 72 108 144 180 216 252 288 324 360 ....
Multiples de 48	-48 -96 -144 -192 -240 -288 -336 -384 -432 -480 .... 48 96 144 192 240 288 336 384 432 480 ....

La notion de PPCM est alors victime de son sens premier. En effet, -288 est clairement un multiple commun à 36 et 48. Qui plus est, il est inférieur à 144. Même si ce dernier le divise !
Le PPCM doit demeurer le multiple commun le plus "simple" possible. Dans notre exemple, les multiples communs les plus simples sont clairement -144 et 144.

Bref, c'est un beau bordel ! Comme pour le PGCD, nous devons donc donner une nouvelle définition du PPCM pour pouvoir étendre cette notion à .
Cette nouvelle définition est donc la suivante :

Définition (la vraie) du Plus Petit Commun Multiple :
Dire que le nombre m est un Plus Petit Multiple Commun des nombres a et b signifie que :

m est un multiple de a et de b (donc ces deux derniers le divisent).
Si c est un multiple commun de a et de b alors m divise c.

Remarque : Là comme ailleurs, le terme nombre est synonyme d'entiers relatifs vu que nous travaillons dans l'anneau . Mais la présente définition peut être étendue à n'importe quel anneau pourvu qu'il ait les bonnes propriétés...

Le truc en plus : le PPCM de deux entiers relatifs existe-t-il toujours ?
Cette question peut paraître saugrenue. Cependant rien ne garantit que pour tous les couples d'entiers relatifs aient un PPCM avec les conditions fixées par notre définition.
C'est en particulier la condition 2 qui peut faire capoter l'affaire : qu'est-ce qui nous dit qu'un multiple commun divisera tous les autres ?
L'existence d'un tel nombre m d'un PPCM n'est pas acquise !

Cependant, tous les couples d'entiers relatifs non nuls admettent un PPCM.

A l'instar du PGCD, la seconde condition de notre définition fait que deux PPCM d'un même couple (a ; b) se divisent nécessairement mutuellement. Ils sont donc nécessairement associés., c'est-à-dire sont égaux ou opposés...
Ce qui fait que dans , tout couple d'entiers a en tout et pour tout deux PPCM.

Que les multiples communs à deux entiers même relatifs existent, n'est un scoop. Par contre qu'il en existe un avec la seconde condition que nous avons fixée n'a rien d'acquis !

Appelons M⁺(a ; b) l'ensemble des multiples strictement positifs communs à a et b.
La première chose à dire est que ce sous-ensemble de est non vide. En effet, |a.b| en fait partie.
Or tout sous-ensemble non vide de admet un plus petit élément. Appelons-le m.

Nous allons prouver que ce multiple commun m vérifie la seconde condition de notre définition.
Procédons par l'absurde.

Supposons qu'il existe un entier n multiple commun à a et b que m ne divise pas.
Intéressons-nous à sa division euclidienne par m.
Il existe donc un seul couple d'entiers (q ; r) tels que :

n = q.m + r et 0 < r < m

r ne peut pas être nul car m ne divise n.

Comme a divise n et m alors il existe deux entiers k et l tels que :

n = k.a et m = l.a

Revenons à l'égalité découlant de la division euclidienne. Elle devient donc :

n = q.m + r d'où k.a = q.l.a + r d'où r = a . (k - q.l)

a et r étant non nuls, il est clair que a divise r.

En procédant de même et pour les mêmes raisons, on montre que b divise r.

Ainsi donc r est un entier strictement positif qui est un multiple commun à a et b.
Donc r fait partie de M⁺(a ; b).

Arrêtons-nous trente secondes pour reprendre nos émotions et résumer ce que nous avons découvert.

Nous avons établi qu'un élément de M⁺(a ; b) (c'est-à-dire le reste r) était strictement plus petit que le plus petit élément de ce sous-ensemble de .
Ce qui est très fort !

Dans la vie courante, on dirait qu'il y a une couille dans le potage. En maths, on dira que c'est absurde et qu'il y a là une contradiction.
Ce que nous avons supposé est donc faux. Ce qui est donc vrai est son contraire :

Tout multiple commun à a et b est divisé par m.

Donc m vérifie la seconde condition de la définition.

Il existe donc au moins un client pour notre définition. D'où l'existence du PPCM.

Avec notre définition, les deux PPCM de 36 et 48 sont -144 et 144.
De même comme les multiples de -36 sont aussi de 36 alors les couples (-36 ; 48), (36 ; -48) et (-36 ; -48) ont les mêmes PPCM que le couple (36 ; 48) : il s'agit de -144 et 144.

A ce niveau, la seule méthode que nous ayons à notre disposition pour trouver un PPCM de deux nombres est de dresser la liste de leurs multiples et à prendre le plus petit d'entre eux.
A l'instar du PGCD, une autre méthode consiste à décomposer les deux entiers en deux produits de facteurs premiers et à utiliser le théorème suivant :

Théorème : (p_i)_i{1...n} est une famille d'entiers relatifs premiers non associés.

Prenons par exemple encore -36 et 48. Décomposons-les en facteurs premiers. Nous savons déjà que :

-36 = (-1) × 2² × 3² et 48 = 2⁴ × 3

Un PPCM de -36 et 48 est donc 2^sup^(2;4) × 3^sup^(2;1) = 2⁴ × 3² = 144.

Par contre, il n'existe pas (à ma connaissance) d'algorithme d'Euclide pour les PPCM.
Cependant, ayant le PGCD de deux nombres, il est possible de trouver leur PPCM. Cela se fait grâce au théorème suivant :

Théorème liant PPCM et PGCD.
a, b sont deux entiers relatifs quelconques.

Si d est un PGCD de a et b et m un de leurs PPCM alors c le produit d.m est associé au produit a.b

Autrement écrit :

PGCD(a ; b) × PPCM(a ; b) = ± a × b

La preuve de ce théorème.

La démonstration de ce théorème n'est pas à priori évidente. En fait, il suffit juste de connaître le truc...

Soit d un PGCD de entiers a et b.
Cela signifie que d est un diviseur de ces deux entiers.
Donc il existe deux autres nombres a' et b' tels que :

a = d.a' et b = d.b'

La première chose à dire est que a' et b' sont premiers entre deux.
En effet, en utilisant une propriété du PGCD, on peut écrire que :

d = PGCD(a ; b) = PGCD(d.a' ; d.b') = d . PGCD(a' ; b')

D'où PGCD(a' ; b') = 1

Nous allons maintenant prouver que l'entier m = d.a'.b' est un PPCM de a et b.

La première condition est de savoir si m est un multiple commun.
Cette question est vite résolue. En effet :

m = d.a'.b' = a.b' = a'.b

La seconde condition précise que p doit diviser tout multiple commun à a et b.
Soit donc z un multiple commun à a et b.
Essayons de voir quelle tête il a !
Comme a et b le divisent, il existe donc deux nombres k et l tels que :

z = k.a = k.d.a' et z = l.b = l.d.b'

Concaténons ces deux égalités. Il vient alors que :

k.d.a' = l.d.b' d'où k.a' = l.b'

car d est non nul vu que c'est un PGCD !

Toujours est-il que maintenant, nous savons que a' est un diviseur du produit l.b'.
Comme a' et b' sont premiers entre eux, en application du lemme de Gauss (sacré lui-même !), nous pouvons affirmer que a' divise nécessairement l.
Donc il existe un nombre q tel que l = q.a'

Quid alors pour notre multiple commun ? Et bien, il devient ce qui suit :

z = l.b = q.a'.d.b' = q.m

Ainsi donc m divise z.

Autrement écrit, m divise tout multiple z commun à a et b.
La seconde condition de la définition est donc remplie.
Donc m est un PPCM pour a et b. De plus :

d.m = d.a'.d.b' = a.b

Sachant que dans l'anneau , le PGCD et le PPCM sont uniques au signe près (à l'association près), nous avons prouvé le théorème.

Ce théorème a trois conséquences sur le PPCM : la première concerne le PPCM de deux nombres premiers entre eux, la seconde est une propriété, la dernière un moyen indirect de le calculer.

PPCM de nombres premiers entre eux.
Si deux nombres a et b sont premiers entre eux alors un de leur PGCD est par définition 1.
En application de notre théorème, il vient alors que leur PPCM est nécessairement égal à leur produit a.b.

La propriété.

Propriété : si a, b et k sont trois entiers relatifs quelconques alors :

PPCM(k.a ; k.b) = k . PPCM(a ;b)

Cette propriété découle directement de l'application du théorème à k.a et k.b ainsi que d'une propriété similaire du PGCD. En effet :

k² . PGCD(a ; b) × PPCM(a ; b) = k².a.b = PGCD(k.a ; k.b) × PPCM(k.a ; k.b) = k.PGCD(a ; b) × PPCM(k.a ; k.b)

Une des utilisations de cette propriété est la détermination d'un PPCM par la recherche de facteurs communs. C'est un peu abstrait aussi donnons un exemple avec 56 et 84.

PPCM(56 ; 84)	= PPCM(4×14 ; 4×21)	car 56 et 84 sont divisibles par 4.
	= 4 × PPCM(7×2 ; 7×3)	car 14 et 21 sont dans la table de 7
	= 28 × PPCM(2 ; 3)	2 et 3 sont premiers entre eux...
	= 28 × 6 = 168

Nous avons vu une méthode similaire avec le PGCD. Cette méthode est efficace à condition de connaître ses tables et quelques tests de divisibilités comme ceux par 2, 3, 5 et 9...

Le calcul pratique du PPCM.
L'algorithme d'Euclide est un moyen rapide permettant de déterminer le PGCD de deux nombres. Avec le théorème, nous pouvons alors trouver leur PPCM. En effet nous savons désormais que : C'est d'ailleurs sur cette formule que repose l'applette suivante.

L'applette déterminant les PPCM de deux entiers relatifs.
Déterminons les PGCDs de et de .

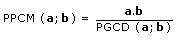
Car ainsi vont les PPCM dans .

En guise de conclusion.
Nous avons été bien au-delà de tout ce qui est demandé en Terminale Scientifique. Dans ce chapitre comme Juste au-delà de Z, nous avons essayé de vous faire sentir et comprendre qu'au-delà de quelques propriétés d'arithmétiques, il y avait l'algèbre. Mais cela est une autre aventure...

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Juin 2001/Janvier 2003. Tous droits réservés.