L'arithmétique commence à être abordée en Troisième. Puis elle s'estompe jusqu'en Terminale. Elle demeure alors l'apanage des scientifiques spécialité maths. Elle préfigure cependant les structures algébriques qui seront abordées après le Bac. Cette page s'adresse à tous les élèves de TS spé maths et à tous les curieux qui veulent aller plus loin, au-delà de . Pour en savoir plus sur certains sujets, déplacer votre curseur sur le logo ...

Une introduction au-delà de .
est une vielle connaissance. C'est en effet cet ensemble des entiers relatifs que nous connaissons depuis la cinquième. Il renferme tous les entiers qu'ils soient négatifs, positifs ou nul.
Mais d'un point de vue algébrique, est plus que tout cela !

D'un point de vue algébrique, est un ensemble sur lequel ont été définies deux Lois de Composition Internes, c'est-à-dire deux opérations à partir desquelles tout se fait !

• La première de ses LCI est l'addition.
  Pour cette opération, est un ensemble quasiment parfait !
  En effet, l'élément neutre de l'addition fait partie de .

  Dire qu'un nombre e est un élément neutre pour l'opération + signifie que pour tout nombre x, on a : e + x = x + e = x.   L'élément neutre de l'addition est 0 alors que celui de la multiplication est 1. L'élement neutre pour la composition des fonctions est la fonction Id(x) = x.

  
  Ensuite est stable pour l'addition. Autrement dit, la somme de deux entiers relatifs en est un autre.
  Enfin chaque entier relatif a un collègue qui est son opposé pour l'addition.

  Autrement dit : Pour tout nombre a, il existe un nombre b tel que a + b = 0.

  
  Ces trois propriétés font du couple ( , +) un groupe.
   
• La seconde est la multiplication.
  Pour cette opération, est loin d'afficher la perfection précédente. Cependant :
  Pour la multiplication, a un élément neutre qui est 1. Ensuite est stable pour cette LCI : le produit de deux entiers relatifs en est un autre.
  Par contre, n'offre pas à tous ses membres un "opposé" (c'est-à-dire un inverse) pour cette multiplication. En effet, l'inverse de 2 qui est 0,5 ne fait pas partie de .
  Ainsi ( , ×) n'est pas un groupe !
  Par contre, la multiplication est distributive par rapport à l'addition.

  C'est-à-dire que si a, b et c sont trois nombres alors : a . (b + c) = a.b + a.c = (b + c) . a

  
  Cette propriété ajoutée aux autres, fait de ( , + , ×) un anneau.
   

Ce sont là des considérations algébriques qui ne prennent leurs sens qu'après le Bac. Mais l'arithmétique et l'ensemble préfigure ce que sont les structures algébriques...

Remarque : Peut-être avez-vous compris qu'il fallait que l'élément neutre de la multiplication 1 fasse partie de pour que ce dernier fût un anneau. En fait, ce n'est pas indispensable. Mais lorsque c'est le cas (comme pour ), on dit alors que l'anneau est unitaire...

Autre remarque : Seuls deux entiers relatifs peuvent être inversés dans . Il s'agit de -1 et 1. Quand dans la suite, nous évoquerons les inversibles de , c'est d'eux deux que nous parlerons !

Le truc en plus : Beaucoup d'ensembles sont des anneaux. Vous en connaissez d'ailleurs un certain nombre ! Parmi eux, il y a l'ensemble des rationnels , celui des réels , celui des complexes et celui des quaternions . Ce sont des anneaux pour les mêmes lois de composition que ! Pourtant ils ont un truc un plus : dans chacun d'entre eux tout nombre non nul a un inverse pour la multiplication. Cette propriété fait d'eux des corps. Parmi les autres anneaux que nous évoquerons dans la suite, il y a aussi  [i] qui est l'ensemble des nombres complexes  a + i.b  où  a et b sont deux entiers relatifs. La somme, la différence ou le produit de ces "complexes entiers" en est clairement un autre. Il n'y a qu'à voir ce qui se passe avec certains de ces nombres comme  2 + 3i   ou   5i   ou   6 -7i   ou  5. Il est aisé de démontrer que ([i], + , ×) est un anneau. Dans le même ordre d'idée on peut aussi évoquer le cas de [] qui est un anneau pour les mêmes lois. C'est l'ensemble des nombres de la forme  a + b.  où a et b sont deux entiers relatifs. Parmi les nombres composant cet ensemble il y a :  0  ,  2 + 5. ,  -3  ,    ,  7 - 3.  et bien d'autres...

Des notions au-delà de .
Nous l'avons dit et redit : préfigure ce que sont les structures algébriques. Pour celles-ci, on définit des notions qui se retrouvent confondues dans l'anneau . Nous allons à présent les évoquer. A cette occasion, nous bouleverserons certaines idées reçues.

1. La divisibilité.
   Cette définition est plus ou moins consciemment connu depuis la sixième...
     

   Définition : Dire que le nombre a divise le nombre b signifie qu'il existe un nombre c tel que :b = a . c

   Ainsi 7 divise 42 car  42 = 7 × 6. 
   De même -7 est un autre diviseur de 42 car   42 = (-7) × (-6).
   Dans <, un diviseur, un dividende ou leur quotient peuvent être positifs, négatifs voire nul..

2. Des nombres associés.
   Voilà une notion nouvelle et peu compliquée qui nous servira de manière pratique...
    

   Définition : Dire que deux nombres a et b sont associés signifie qu'ils se divisent mutuellement.

   Dans , deux nombres distincts sont associés lorsqu'ils sont opposés.
   C'est par exemple le cas du couple 23 et -23. En effet : -23 = 23 × (-1)  et  23 = (-23) × (-1)

   Note : à l'image de ce qui se passe dans , on montre facilement que si deux nombres sont associés alors on passe de l'un à l'autre en le multipliant par un inversible. Dans , il s'agit de -1 ou de 1.

   Soient a et b deux nombres associés. Ils se divisent donc mutuellement. Comme a divise b alors il existe un nombre x tel que a . x = b. De même comme b divise a, il existe donc un nombre y tel que b . y = a Combinons ces deux égalités. Il vient donc que : Un produit est nul si et seulement si l'un de ses facteurs l'est. Comme b a été supposé non nul, cela implique que y.x - 1 l'est nécessairement. De là, comme le produit y.x vaut 1, cela veut donc dire que x et y sont inversibles. Conclusion : si deux nombres sont associés alors on passe de l'un à l'autre en le multpliant par un inversible. Certains disent que deux nombres sont associés s'ils sont égaux à l'inversible près.

3. Les nombres premiers.
   En troisième, on vous a donné une certaine définition des nombres premiers. Ce sont ceux qui ne sont divisibles que par 1 ou eux-mêmes. Seulement, c'est là la définition d'une autre notion. La vraie définition d'un nombre premier est ce qui suit...
    

   Définition : Dire que le nombre a est premier   signifie que   s'il divise un produit b.c  alors il divise b ou il divise c.

   Par exemple, 7 est un nombre premier. En effet, quelque soit le produit divisible par 7 que l'on prenne, il en divisera toujours l'un des facteurs. Essayez 14, 35 ou -42...
   De même, -7 est également un autre nombre premier !
   Par contre, 6 n'est pas premier. En effet, bien que 6 divise  24 = 3 × 8 ,  il ne divise ni 3, ni 8.  

   Remarque : les nombres premiers peuvent être positifs ou négatifs. On considère que les nombres inversibles ne peuvent pas être considérés comme premier. Il en va de même pour 0.

4. Les nombres irréductibles.
   Ce que l'on vous présentait comme la définition de la priméralité est en fait celle de l'irréductibilité.
    

   Définition : Dire que le nombre a est premier signifie que les seuls nombres le divisant sont ceux que l'on peut inverser et ceux qui lui sont associés.

   Si nous avions travaillé dans l'ensemble des entiers naturels , il aurait suffi de dire :

   ...ses seuls diviseurs sont 1 et lui-même.Seulement nous sommes dans  et notre volonté est d'être le plus précis possible...

   Par exemple, 31 et -31 sont irréductibles car ses seuls diviseurs sont les inversibles -1 et 1 ainsi que les deux nombres qui lui est associé : -31 et lui-même !

   Dans le cas particulier de l'anneau , les notions de priméralité et d'irréductibilité sont équivalentes. C'est pour cela que l'on confond ces deux notions !
   Mais il est des anneaux où il en va différemment.

Un premier truc en plus : les nombres premiers sont irréductibles. Nous avons dit dans la présentation de nos quatre notions que dans l'irréductibilité et la priméralité étaient des notions équivalentes. Cependant cette équivalence est fausse en générale ! La seule chose qui soit vraie quelque soit l'anneau considéré est que :   Si un nombre est premier  alors  il est irréductible Mais la réciproque est fausse ! Pour connaître le pourquoi du théorème déplacez votre curseur ici.

p est un nombre premier. Supposons qu'il ait des diviseurs c'est-à-dire que p soit un produit. Il existe donc deux nombres a et b tels que p = a . b On peut aussi utiliser cette égalité pour dire que p divise le produit a.b. En effet, on a bien que : a.b = p × 1. Or p est un nombre premier, donc s'il divise un produit, c'est qu'il divise l'un des deux facteurs. Pour fixer les idées, disons qu'il divise a. Comme il divise a, c'est donc qu'il existe un nombre x tel que a = p . x.   La première égalité devient donc : Autrement exprimé, le nombre x est donc l'inverse du nombre b. Ainsi si un nombre premier p est un produit alors l'un des deux facteurs est nécessairement un inversible (ici c'est b). Cela veut dire que l'autre facteur a est nécessairement un nombre associé à p (car x peut être inversé...) Conclusion : les seuls diviseurs de p étant des inversibles et des nombres qui lui sont associés, il est donc irréductible. La priméralité entraîne donc l'irréductibilité...

Un second truc en plus : l'irréductibilité et la priméralité ne se transmettent pas toujours au niveau supérieur !    Revenons aux deux des anneaux de notre introduction : et [i]. Il est clair que le premier est inclus dans le second. Par contre, si se trouve dans les sur-anneaux et , l'anneau [i] est directement plongé dans . Dans l'anneau , 5 est un nombre premier et irréductible. Par contre si l'on se place dans [i] alors 5 perd cette propriété.  En effet dans cet ensemble, on peut écrire que :      5 = (2 - i) . (2 + i)  Tout cela pour dire que lorsque l'on passe à structure supérieure, rien ne garantit qu'un nombre qui était premier ou irréductible, le demeure ! Par contre dans le sens inverse la propriété est conservée : tout entier relatif premier ou irréductible dans [i] l'est de facto dans . La question que tout le monde se pose : C'est quoi au fait les premiers/irréductibles de [i] ?

Quelques mots sur [i] Les inversibles de [i] sont -1, 1, i et -i. Pour être irréductibles/premiers dans [i], il faut être ou être associé à : un entier positif dont le reste de leur division par 4 est égal à 3. Ainsi 7, -7, 7i et -7i sont quatre nombres premiers dans . Ils sont d'ailleurs associés. un nombre de la forme a + i.b dont le carré du module a2 + b2 est premier dans . Ainsi 2+i et 2i-1 sont premiers dans [i]. Ils sont aussi associés.

Décomposition en facteurs premiers.
comme comporte une infinité de nombres premiers/irréductibles. A partir de ceux-ci, on peut exprimer n'importe quel entier sous la forme d'un produit : c'est la décomposition en facteurs premiers...
Nous commencerons par parler de la décomposition en facteurs premiers d'un entier naturel avant de conclure plus généralement sur les relatifs.

Théorème de la décomposition en facteurs premiers dans . Tout entier naturel supérieur à 1 peut s'écrire comme étant le produit de nombres premiers.

Voyons sur un exemple ce que signifie ce théorème.
Par exemple, il dit que 24 peut être écrit sous la forme d'un produit d'entiers naturels premiers. En effet :

24 = 2 × 2 × 2 × 3 = 2³ × 3

2 et 3 sont des nombres premiers ou irréductibles. Ils servent à décomposer 24.

Ce théorème a beau être assez court, il nous faut pourtant le démontrer car même si cela marche avec 24, rien ne garantit qu'il soit vrai ailleurs !
Rappelons que 1 n'est pas considéré comme un nombre premier/irréductible !

Cette propriété établie pour les entiers naturels peut être étendue sur . En effet, prenons un entier relatif z quelconque. Il y a alors plusieurs cas possibles :

• z est égal à -1 ou 0 ou 1 : il y a là deux inversibles et 0. Or nous l'avons dit : ceux-ci sont hors jeu.
    
• z est un entier positif supérieur ou égal à 2 : à ce moment-là, nous sommes dans le cas de décomposition en facteurs premiers dans .
    
• z est un entier négatif inférieur ou égal à -2 : le nombre -z est alors un entier naturel. Il peut s'écrire comme un produit de facteurs premiers. Quant à z, on peut comme étant le produit de l'inversible -1 et de nombres premiers. On peut donc le décomposer !

Cela nous donne le théorème suivant :

Théorème de la décomposition en facteurs premiers dans . Tout entier relatif non nul et non inversible (différent de -1 et 1) est le produit d'un inversible et de nombres premiers/irréductibles.

Autrement écrit, tout entier relatif z peut être décomposé sous la forme :

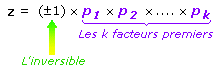
Intéressons-nous par exemple à -24. Le théorème dit qu'on peut le décomposer. En effet, on peut écrire que :

-24 = (-1) × 2³ × 3 = 1 × (-2)³ × 3 = 1 × 2³ × (-3) = (-1) × (-2)³ × (-3)  

Ce sont là trois décompositions de -24. En effet -3, -2, 2 et 3 sont des nombres premiers/irréductibles dans .
Nous aurions pu être plus vicieux en exhibant la décomposition :  -24 = (-1) × 2 × (-2) × 2 × (-3).
C'est une autre décomposition de -24 en facteurs premiers.
De même, on peut décomposer 24 dans sous la forme :   24 = (-2) × 2 × 2 × (-3).

Tout cela pour dire qu'il y a plusieurs façons d'écrire une décomposition en facteurs premiers. Pour n'en avoir qu'une seule, un usage consiste à ne prendre que des entiers premiers positifs. Pour nos deux exemples, les décompositions en facteurs premiers pédagogiquement correctes sont donc :

24 = 1 × 2 × 2 × 2 × 3 = 2³ × 3      et      -24 = (-1) × 2³ × 3

L'applette : Comme on est sympa, nous vous proposons de décomposer l'entier relatif .

Le truc en plus : le fait que tout entier différent de -1, 0 ou 1 soit décomposable en un produit de facteurs premiers fait de un anneau factoriel.

La division euclidienne dans .
Pour terminer cette page, nous allons évoquer la division euclidienne. Non dans mais dans l'ensemble des entiers relatifs .

La division euclidienne est une vieille connaissance : tout du moins dans . Chacun a appris à l'école primaire à poser et effectuer des divisions. "En tant, combien de fois..." telle était la phrase mythique ruminée quotidiennement par cette si belle institutrice d'alors. Puis l'aventure s'est poursuivi au collège.
Mais aujourd'hui les choses ont changées. Il ne s'agit plus d'entiers simplement naturels mais de relatifs. Et là les choses deviennent plus mathématiques !

On pourrait croire que la division euclidienne a été donné aux hommes par Dieu avec les dix commandements. En fait, elle est la conséquence d'un théorème dans comme dans . 

Théorème : la division euclidienne dans . Si a et b sont deux entiers relatifs (b étant non nul)  alors  il existe un et un seul couple d'entiers relatifs (q ; r) tels que :a = b.q + r    et     0 r < |b| On dit que la division euclidienne du dividende a par le diviseur b a pour quotient q et pour reste r.

Nous verrons un peu plus tard ce que signifie diviser euclidiennement deux entiers relatifs. A présent, il nous faut démontrer ce théorème. Car rien ne garantit qu'il soit vrai pour tous même s'il marche ici et là !

Ce superbe nous dit qu'il est possible d'étendre la division euclidienne de à . Seulement il ne nous dit pas comment procéder avec des entiers négatifs. Nous pourrions traiter quelques exemples mais ce n'est pas ce que nous ferons.
Si vous voulez savoir comment diviser euclidiennement dans , expérimentez donc avec l'applette ci-dessous !

L'applette : Comme on est sympa, nous vous proposons d'effectuer la division euclidienne de .

Le truc en plus : La division euclidienne fait de l'anneau un anneau euclidien.

En guise de conclusion : on pourrait croire que la division euclidienne est spécifique aux entiers. En fait, il n'en est rien. Nous avons déjà vu qu'il existait une division euclidienne pour les polynômes. Le théorème présidant à celle-ci est le suivant :

Cette division euclidienne fait de l'ensemble des polynômes à coefficients réels [X] un autre anneau euclidien...

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Avril 2001/Janvier 2003. Tous droits réservés.