Le barycentre des points pondérés 
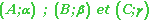
est le point du plan défini par la relation vectorielle :
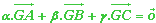
Pour que ce barycentre G existe, la somme des trois coefficients de pondération doit être non nulle. Suivant les valeurs prises par les trois coefficients de pondération, la position du point G varie. Lorsque les trois coefficients sont égaux et non nuls, le point G est l'isobarycentre des points A, B et C, c'est-à-dire le centre de gravité du triangle ABC. Lorsque les trois coefficients de pondération ont le même signe, le barycentre G est à l'intérieur du triangle ABC. Dans le cas contraire, il se trouve à l'extérieur. Lorsque l'on multiplie les trois coefficients de pondération par le même facteur, la position du barycentre G ne change pas.
Ainsi le barycentre des points pondérés (A;1), (B;2) et (C;3) est aussi celui des points pondérés (A;2), (B;4) et (C;6).