Les
fractions : les bases
Les fractions ne sont pas une nouveauté
pour toi car tu les as vu en Sixième. Il s'agissait alors de fractions sur 10,
100 ou 1000.
Dans cette page, nous verrons qu'une fraction peut être sur n'importe quoi !
C'est quoi une fraction ?
Certains divisions tombent justes. C'est par exemple le cas de la
division 45 ÷ 18 qui donne 2,5.
D'autres ne s'arrêtent jamais. C'est ce qui se produit avec 19 ÷ 3 =
6,333333333...
Pour que ces dernières aient un résultat, on crée une nouvelle espèce de
nombre : les fractions.
Le résultat de la division 19 ÷ 3 est le nombre  .
Une valeur approchée de cette fraction
est 6,333333333.
.
Une valeur approchée de cette fraction
est 6,333333333.
En fait, tous les nombres que nous connaissons,
sont des fractions. Même si parfois, ils se
cachent. Regardons cela en détail.
- Tous les entiers sont des fractions.
Ainsi par exemple, 3 est une fraction !
En effet 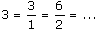
- Tous les décimaux sont des fractions.
Par exemple, 4,51 et 0,241 sont des fractions
car  et
et 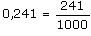 .
.
Egalité de deux fractions.
Comme nous l'avons entrevu dans le précédent
paragraphe, deux fractions
dont l'écriture est différente peuvent être égales.
C'est par exemple le cas de 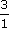 et
et 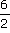 qui sont égales à 3.
qui sont égales à 3.
|
Le problème est donc le suivant :
Quand on a
deux fractions apparemment différentes, comment peut-on savoir si elles sont
égales ou non ?
|
Pour répondre à cette question, nous allons
nous intéresser aux trois fractions.
Prenons par exemple 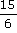 ,
,
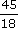 et
et 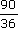 .
.
Une fraction est par définition le résultat d'une division. Effectuons les
trois divisions correspondantes :
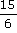 = 15 ÷ 6 = 2,5 = 15 ÷ 6 = 2,5 |
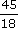 = 45 ÷ 18 = 2,5 = 45 ÷ 18 = 2,5 |
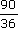 = 90 ÷ 36 = 2,5 = 90 ÷ 36 = 2,5 |
Comme ces trois divisions donnent le même
résultat, nous pouvons donc dire que ces trois fractions sont égales.
Mais qu'ont donc de communs ces trois fractions ?
Examinons séparément leurs numérateurs et
leurs dénominateurs :
| Numérateur |
15 |
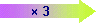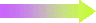 |
45 |
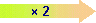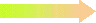 |
90 |
|
|
|
|
|
|
| Dénominateur |
6 |
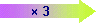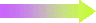 |
18 |
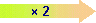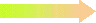 |
36 |
Pour passer de 15
à 45, on multiplie par la même chose que
pour passer de 6 à 18.
Autrement dit, ces deux fractions sont égales car pour passer de l'une à
l'autre, on multiplie le numérateur et le dénominateur
de la première fraction par un même
nombre : 3.
Et c'est pareil pour la doublette 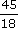 et
et 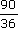 .
Pour passer de l'une à l'autre,
on multiplie numérateur et dénominateur par 2.
.
Pour passer de l'une à l'autre,
on multiplie numérateur et dénominateur par 2.
Nous tenons là notre règle.
Règle : Reconnaître deux
fractions égales
Deux fractions sont égales lorsque
pour passer de l'une à l'autre, on multiplie ou on divise ses
numérateurs et dénominateurs par un même nombre. |
Ainsi avec notre exemple :

Simplifier une fraction.
Simplifier une fraction, c'est
trouver la fraction égale à cette
première qui a les plus petits numérateur
et dénominateur possibles.
Par exemple, la forme simplifiée de la
fraction 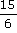 est
est 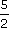 . .
On ne peut pas trouver de plus petits numérateur et dénominateur que 5
et 2. |
Comparer deux fractions.
Comparer deux fractions, c'est dire laquelle est la plus grande, quelle est
la plus petite.
Pour cela, il n'existe pas de règle générale. Seulement des trucs que nous
allons aborder.
- Les deux fractions ont le même
numérateur.
Lorsque deux fractions ont le même numérateur,
la plus grande est celle qui a le dénominateur le
plus petit.
Par exemple, 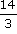 est plus grand que
est plus grand que 
En effet, le dénominateur 3 est plus
petit que le dénominateur 8.
C'est l'histoire du partage de 14 francs entre 3 ou 8 personnes. Dans
quel cas la part sera-t-elle la plus grosse ?
- Les deux fractions ont le même
dénominateur.
Lorsque deux fractions ont le même
dénominateur, la plus grande est celle qui a le
plus grand numérateur.
Par exemple, 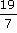 est plus grand que
est plus grand que 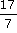 .
.
En effet, le numérateur 19 est plus grand que le numérateur 17.
C'est logique car plus il y a à se partager et plus chacun aura !
- Comparer une fraction par rapport à 1.
Une fraction dont le numérateur
est plus petit que le dénominateur,
est plus petite que 1.
Par exemple, 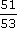 est plus petit que 1.
est plus petit que 1.
Une fraction dont le numérateur est
plus grand que le dénominateur,
est plus grande que 1.
Par exemple, 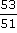 est plus grand que 1.
est plus grand que 1.
En conclusion, nous pouvons dire que : 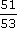 < 1 <
< 1 < 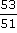 Donc la fraction
Donc la fraction 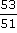 est plus grande que
est plus grande que 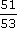 .
.
- La méthode qui marche tout le temps : effectuer la division.
En effet, une fraction est avant tout le résultat d'une division.
On peut donc toujours essayer cette méthode même si elle n'est pas
toujours la plus facile !
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par
la taverne de l'Irlandais.
(c) Mai 2000/Janvier 2003. Tous droits réservés.

 .
Une valeur approchée de cette fraction
est 6,333333333.
.
Une valeur approchée de cette fraction
est 6,333333333. est le quotient de a par b.
est le quotient de a par b.

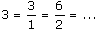
 et
et 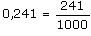 .
.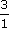 et
et 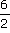 qui sont égales à 3.
qui sont égales à 3.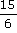 ,
,
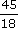 et
et 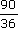 .
.
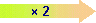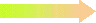

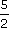 .
.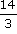 est plus grand que
est plus grand que 
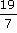 est plus grand que
est plus grand que 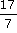 .
.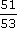 est plus petit que 1.
est plus petit que 1.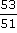 est plus grand que 1.
est plus grand que 1.