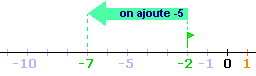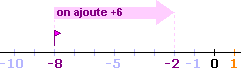Au sommaire : Quelques rappels Additionner Opposé Soustraire Nouveautés

Tu as commencé à aborder les nombres relatifs en Sixième. Nous rappellerons dans un premier temps ce que tu es sensé savoir. Puis nous nous attaquerons à l'addition à la soustraction de ces nombres relatifs...

 

Quelques rappels.
Jusqu'en Sixième, l'on ne connaissait que les nombres positifs comme 1 ou 676,45.
Seulement dans la vie, il n'y a pas qu'eux. Il n'y a qu'à prendre l'exemple d'un thermomètre.

Lorsque la température est à 14° au-dessus de 0, alors il fait assez chaud. On dit alors que la température est de 14° et qu'elle est positive.

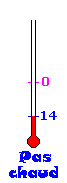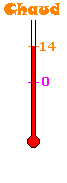
Par contre, lorsqu'elle descend à 14° au-dessous de 0, il ne fait pas chaud du tout ! On dit que la température est de -14° et qu'elle est négative.

Dans la vie, à part les nombres positifs, il y a donc aussi les nombres négatifs. 
Ces deux espèces de nombres sont des nombres relatifs.

Ce que tu dois savoir sur les nombres relatifs :
Les nombres relatifs sont :

  • les nombres négatifs comme -4 ou -2,45.
    Ils se trouvent à gauche de 0 sur la droite graduée.

  • Le nombre 0 qui n'est ni négatif, ni positif.

  • Les nombres positifs comme 2 ou 7,31.
    Ils se trouvent à droite de 0 sur la droite graduée.

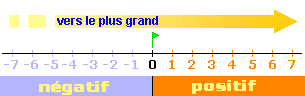
Lorsque l'on a deux nombres relatifs a et b :

  • Le plus grand des deux est celui qui sur la droite graduée est le plus à droite.

  • Le plus petit des deux est celui qui est le plus à gauche.

Ainsi :

 

Additionner  des nombres relatifs.
Additionner deux nombres positifs ne pose aucun problème. Chacun sait faire 3 + 12.
Par contre, nous ne savons pas faire les additions  (+3) + (-12)  et  (-2) + (-5) ?
Pour y parvenir, nous allons nous aider de la droite graduée.

Regardons à quoi correspond sur la droite graduée, l'opération  (+3) + (+12).

Intéressons-nous à présent à l'opération  (+3) + (-12).
Si lorsque l'on ajoute +12 alors on avance de 12 cases.
Donc ajouter -12 revient à reculer de 12 cases...

Ainsi :

Effectuons l'opération  (-2) + (-5)

Sur la droite graduée, nous nous positionnons en -2.
Puis nous ajoutons -5 : c'est-à-dire que nous reculons de 5 unités.
Comme nous arrivons en -7 alors

(-2) + (-5) = -7

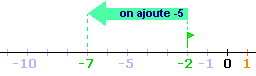De la même manière :

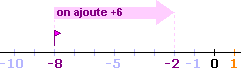Pour effectuer sur la droite graduée l'opération
(-8) + (+6), il faut :
  • se positionner en -8.
  • avancer de 6 unités.

Comme l'on arrive en -2 alors   (-8) + (+6) = -2.

Ces petits trucs avec la droite graduée, c'est bien beau mais ce n'est pas une règle.
La règle ci-dessous décrit la démarche pour additionner deux nombres relatifs.

Règle : Comment additionner deux nombres relatifs ?
La valeur absolue d'un nombre relatif est ce nombre sans son signe.
Par exemple, la valeur absolue de +4 est 4. Celle de 0 est 0 et celle de -2 est 2.

Pour calculer la somme de deux nombres relatifs, on doit envisager plusieurs cas :

  1. Si ils sont positifs alors on effectue une addition classique.
    Par exemple,  (+3) + (+12) = 3 + 12 = 15.
    La somme de deux positifs est toujours positive.
     
  2. Si l'un est négatif et l'autre est positif alors leur somme peut être négative ou positive.
    Pour la calculer, on procède de la manière suivante.
    Par exemple : Calculons (+3) + (-7).
    La valeur absolue de +3 est 3. Celle de -7 est 7.
    La différence de leurs valeurs absolues vaut : 7 - 3 = 4.
    Comme 7 (qui vient de -7) est plus grand que 3 (qui vient de +3) alors le résultat de l'addition est négatif  car  il y a "plus de négatif que de positif".
    Donc  (+3) + (-7) = -4  
    Par contre,   (-4) + (+5) = 1  car il y a plus de positif que de négatif.
        
  3. Si a et b sont négatifs alors la somme a + b est elle aussi négative.
    Pour la calculer, on procède de la manière suivante :
    Par exemple, calculons (-4) + (-6) :
    La somme des valeurs absolues vaut : 4 + 6 = 10
    Donc (-4) + (-6) = -10.
Maintenant c'est à toi de montrer que tu as compris comment fonctionnait l'addition !
 

 

Opposé d'un nombre relatif.
L'opposé d'un nombre relatif est celui qui sur la droite graduée se trouve à l'opposé par rapport à 0.
Par exemple, l'opposé de 5 est -5.


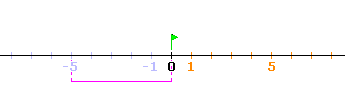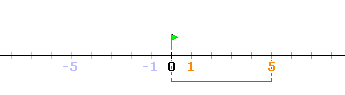
Par rapport à 0, -5 est à l'opposé de 5.
De même, on peut dire l'opposé de -5 est 5.

Cette vision de l'opposé avec la droite graduée est une vision pratique. En fait, la véritable définition de l'opposé d'un nombre relatif est la suivante :

Définition : Opposé d'un nombre relatif.
L'opposé d'un nombre relatif a est le nombre relatif b qui ajouté à a est égale à 0
 
c'est-à-dire tel que  a + b = 0

Cette définition dit la même chose que ce que nous disions avec notre vision pratique. 
En effet, comme (-5) + (+5) = 0, alors d'après la définition l'opposé de 5 est bien -5.
Et réciproquement...

 

Soustraire deux nombres relatifs.
Nous allons énoncer dans ce paragraphe une chose que tu retrouveras tout au long de tes activités mathématiques : la soustraction est une addition particulière...

Définition : soustraction de deux nombres relatifs.
Soustraire un nombre relatif à un autre, c'est y ajouter l'opposé de ce premier.

c'est-à-dire que :  a - b = a + opposé de b

Voyons sur quelques exemples, ce que cela donne :

Rien de bien compliquer ! Celui qui sait additionner deux nombres relatifs, sait aussi les soustraire.

Maintenant c'est à toi de montrer que tu as compris comment on soustrait...
 

 

Nouveautés : vers de nouvelles écritures.
Il est très rare que l'on écrive une addition ou une soustraction sous la forme que nous avons utilisée. Il est vrai que l'écriture  (+5) + (-3) est assez lourde !
Dans la pratique, on retrouve plutôt les choses suivantes :

5 + 3 au lieu de (+5) + (+3)    
5 - 3 au lieu de (+5) + (-3) ou (+5) - (+3)
-5 + 3 au lieu de (-5) + (+3)    
-5 - 3 au lieu de (-5) + (-3) ou (-5) - (+3)

En lieu et place de nos parenthèses d'avant, nous utiliserons désormais une écriture simplifiée et plus légère.

Mais globalement, cela ne changera rien !

Pour terminer cette page sur les nombres, nous allons parler des "règles de signe". Par exemple, à quel nombre relatif est égal  -(-2) ?
Nous avons déjà répondu partiellement à la question avec la soustraction.

Règles de signe :
Si a est un nombre positif  alors :
 
+(+a) = +a
Par exemple,  +(+5) = 5.		 +(-a) = -a
Par exemple,  +(-5) = -5.
-(+a) = -a
Par exemple,  -(+5) = -5.		 -(-a) = +a
Par exemple,  -(-5) = +5.
 
Deux signes plus ou deux signes moins donnent un plus.
Deux signes différents donnent un moins.

Ces règles de signe sont à savoir par coeur. On peut les utiliser par exemple dans les deux exemples suivants :

Calculons ce qui suit :

-4 - (-5)= -4 + 5 = 1

-(-4) - 5 = 4 - 5 = -1

 Calculons  -(-7) + (-9) - 8 :
 
-(-7) + (-9) - 8  = 7 + (-9) - 8
 = 7 - 9 - 8
 = -2 - 8 
 = -10

Dans ces trois exemples, avant de tout calculer, il faut simplifier les opérations...

A présent, c'est à toi de montrer que tu as compris ce dont nous venons parlé...
 
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) Mai 2000/Janvier 2003. Tous droits réservés.