La fonction cube est la fonction définie par :

La première chose à faire est de déterminer l'ensemble de définition de notre fonction.

Le cube de tout réel étant défini (ce n'est rien d'autre qu'une double multiplication ! ), l'ensemble de définition de la fonction f est R.

La principale propriété de la fonction cube est son imparité.

En effet si x est un réel alors

Ce qui prouve bien que la fonction soit impaire.

La première conséquence de celle-ci est que l'origine sera pour la courbe un centre de symétrie.

Représentation graphique de la fonction cube sur l'intervalle [-4,7 ; 4,7].

• Comme annoncé au paragraphe précédent, la courbe admet l'origine comme centre de symétrie.
• A son extrémité gauche, la courbe semble plonger vers l'infiniment négatif. On dit alors que lorsque x tend vers -, f(x) tend aussi vers -. Ou encore que f a pour limite - en -.
• A son extrémité droite, la courbe semble s'envoler vers l'infiniment positif. On dit alors que f(x) tend vers + lorsque x tend vers +. On dit aussi que la limite en + de la fonction f est +.
• Comme le montre le tracé suivant, à l'approche de 0, la courbe se colle de plus en plus à l'axe des ordonnées. Elle s'en décolle ensuite au même rythme. On dit que l'axe des abscisses est tangente à la courbe en 0.

Courbe représentative de la fonction cube sur l'intervalle [-1,7 ; 1,7].

Remplissons le tableau de valeurs suivants :

En clair, lorsque x devient grand, f(x) devient énorme ! Ce qui explique l'envolée de la courbe que nous constations avec la représentation graphique.

De la même façon, on constate que plus x devient négativement grand ( sous-entendu x tend vers - ), f(x) devient négativement énorme. D'où le plongeon de la courbe constaté.

Remplissons le tableau de valeurs suivant :

La morale d'un tel tableau est que lorsque x est proche de 0 alors f(x) l'est nettement plus ! Ce qui explique ce collement de la courbe sur l'axe des abscisses que nous constations avec le second tracé.

En observant la courbe, il semble que la fonction soit croissante sur R. Nous allons à présent le montrer en utilisant l'imparité de la fonction cube.

Montrons que f est croissante sur l'intervalle [0 ; + [ qui est aussi l'ensemble des réels positifs.

Soient x et y deux réels positifs tels que x < y.

Par passage de cette inégalité au carré, l'ordre est conservé et donc, il vient alors que : x² < y².

On multiplie alors cette inégalité avec l'inégalité de réels positifs qu'est x < y. C'est le point (ii) du second commandement qui s'applique. Ainsi :

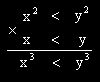
Ainsi si x et y sont deux réels positifs tels que x < y, a-t-on que f(x) < f(y).

f est donc croissante sur l'intervalle [0 ; + [.

Comme de plus f est une fonction impaire alors f est aussi croissante sur l'autre branche de R qu'est ]- ; 0].

En conclusion, f est donc croissante sur tout l'ensemble des réels !

Comme aboutissement de cette quête non pécuniaire, le tableau de variation de la fonction cube s'établit comme suit :

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Septembre 1997/Janvier 2003. Tous droits réservés.