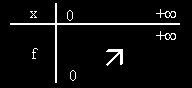La fonction racine carrée.
La fonction racine carrée est la fonction définie par :
Le plan d'étude de la fonction carrée est le suivant :
|
|
On commence par déterminer l'ensemble de définition de la fonction f. C'est-à-dire que l'on cherche l'ensemble des réels ayant une image par la fonction f.
Chacun est normalement sensé le savoir : on ne peut considérer que la racine d'un nombre positif ou nul.
L'ensemble de définition de la fonction racine est donc l'intervalle [0 ; +
[. C'est aussi l'ensemble R+ qui regroupe tous les réels positifs ou nuls.
Représentation graphique de la fonction racine.
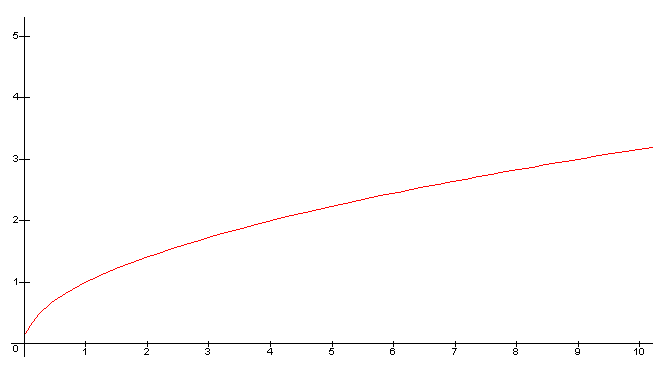
Représentation de la fonction racine sur l'intervalle [0 ; 10]
Commentaires :
, f(x) tend aussi vers + mais à son rythme.
La fonction racine carrée au voisinage de 0.
La courbe semble bien de plus en plus coller à l'axe des ordonnées au fur et à mesure qu'on se rapproche de 0.
Comportements de la fonction racine carrée.
Remplissons le tableau de valeurs suivant :
| x | 1 | 100 | 104 | 102.n |
| f(x) | 1 | 10 | 102 = 100 | 10n |
La morale de ce tableau est que lorsque x devient très grand, f(x) devient grand. Ce qui explique cette croissance modérée que nous constations avec la courbe. Ce qui n'empêche pas f(x) qui tendre vers + lorsque x tend vers + .
Variation de la fonction racine carrée.
La courbe semble indiquer que la fonction est croissante sur tout son ensemble de définition. Montrons-le !
Soient x et y deux réels positifs tels que x < y.
Par passage de cette inégalité à la racine carrée, l'ordre se conservant, il vient que :
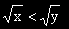
Ainsi a-t-on que f(x) < f(y).
Autrement dit, la fonction f est croissante sur [0 ; +[.
Conclusion de toute cette étude, le tableau de variation de la fonction racine carrée, s'établit comme suit :
