Sens de variation et extréma.
Le sommaire de cette page est le suivant :
|
Variations d'une fonction.
|
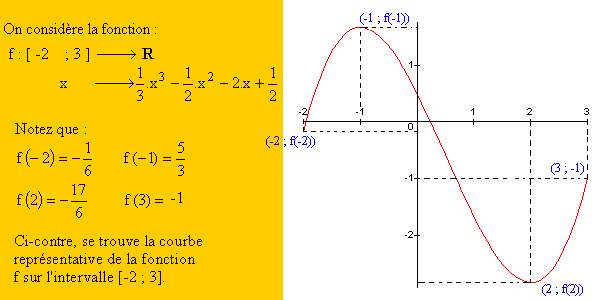
Introduction sur un exemple :
Avant les grandes définitions, nous allons nous exercer sur un exemple...
L'on peut dire de la courbe que :
Nous venons de déterminer graphiquement les variations et les extréma de la fonction f. A partir de ces constats, nous pourrons dresser le tableau de variation de la fonction f sur l'intervalle [-2 ; 3]. Dés que nous saurons de quoi il s'agit !
Si c'est ce que vous avez constaté alors à présent, nous pouvons passer à ces grandes définitions qui vont nous permettre de formaliser ces notions.
Il existe deux types d'extréma : les minima et les maxima.
|
Définition : Soit f : I |
NB : Le minimum d'une fonction est toujours rattaché à un intervalle.
Sur notre exemple, sur l'intervalle [-2 ; 3], f admet un minimum en 2. Ce minimum vaut -17/6.
Par contre, sur l'intervalle [-2 ; 0], f admet un minimum pour x = -2.
|
Définition : Soit f : I |
NB : Comme le minimum, Le maximum d'une fonction est toujours rattaché à un intervalle.
Sur notre exemple, sur l'intervalle [-2 ; 3], f admet un maximum en -1. Ce maximum vaut 5/3.
Par contre, sur l'intervalle [1 ; 3], le maximum est atteint en x = 3.
|
Définition : Soit f : I |
Remarque 1 : La croissance d'une fonction est toujours rattachée à u intervalle. Dans la définition l'intervalle I.
Remarque 2 : Si une fonction est croissante sur un intervalle [a ; b] alors elle atteint son minimum en a et son maximum en b. (Voir dessin).
Sur notre exemple, f est croissante sur les intervalles [-2;-1] et [2 ; 3].
Si l'on observe cette définition, on constate qu'une fonction constante est aussi une fonction constante. En effet, on impose seulement que f(y) soit supérieur ou égal à f(x).
C'est pour les exclure que l'on a instauré la notion de croissance stricte.
On dit qu'une fonction f est strictement croissante sur un intervalle I lorsque si x et y sont deux réels de l'intervalle I tels que x < y alors f(x) < f(y).
Et une fonction strictement croissante est tout simplement croissante.
|
Définition : Soit f : I |
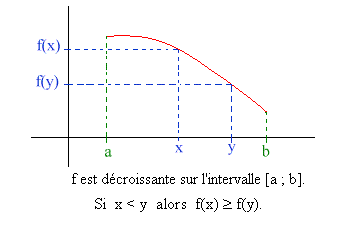
Remarque 1 : La décroissance d'une fonction se fait toujours sur un intervalle. Ici l'intervalle I.
Remarque 2 : Si une fonction est décroissante sur un intervalle [a ; b] alors elle atteint son maximum en a et son minimum en b. (Voir dessin).
Sur notre exemple, f est décroissante sur l'intervalle [-1;2].
Comme précédemment, de part la définition, une fonction constante est aussi une fonction décroissante. C'est pourquoi l'on parle aussi de la décroissance stricte d'une fonction.
On dit qu'une fonction f est strictement décroissante sur un intervalle I lorsque si x et y sont deux réels de l'intervalle I tels que x < y alors f(x) > f(y).
Et comme pour le cas croissant, une fonction strictement décroissante est aussi une fonction décroissante.
Une fois que l'on a déterminé toutes les variations d'une fonction sur son ensemble de définition, on dresse un bilan. C'est ce que l'on appelle un tableau de variation.
Par exemple pour la fonction f qui nous a servi d'exemple d'introduction, celui est :
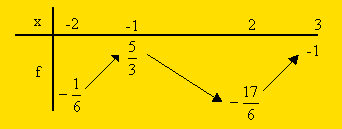
Commentaires :
, une fonction définie sur un intervalle I. a est un réel de l'intervalle I.
f(a).
f(a).