Quand on travaille dans le plan, deux droites qui ne sont pas sécantes, sont dites parallèles. Elles peuvent être parallèles confondues ou parallèles distinctes.
Dans l'espace, on retrouve la même chose avec les plans : on dit que deux plans sont parallèles (distincts ou confondus) s'ils ne sont pas sécants. C'est de cette façon que l'on définit le parallélisme...
Le parallélisme de deux plans se définit comme suit :

L'intersection d'une droite et d'un plan est un point si ce second ne contient pas cette première. On dit alors que la droite et le plan sont sécants.
S'ils ne sont pas sécants, on dit qu'ils sont parallèles.
Le parallélisme d'un plan et d'une droite se définit comme suit :

Ces parallélismes présentent certaines propriétés. Enonçons-les.
Chaque propriété est démontrée et illustrée par un exemple dans le cube en vision réel.

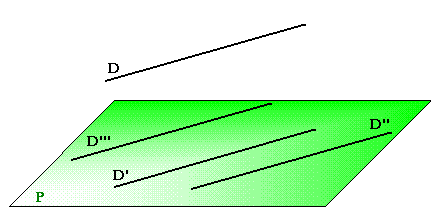Comme la droite D est parallèle au plan P alors elle est parallèle à au moins une droite de ce dernier. Ce peut être D', D'' ou D'''.

La droite D est parallèle à la droite D' qui est incluse dans le plan P. Donc D est parallèle à P.

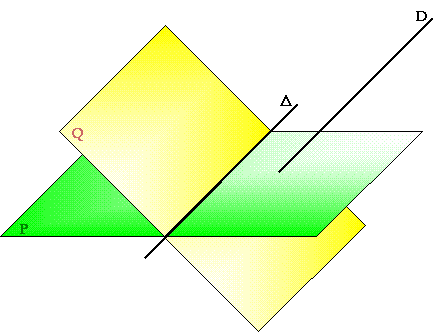
La droite est parallèle aux plans P et Q. L'intersection de ces derniers étant la droite , D y est donc parallèle.

D1 et D2 sont deux droites sécantes du plan P. De même, D3 et D4 sont deux droites sécantes de Q. Comme D1 est parallèle à D3 et qu'il en va de même pour D2 et D4 alors les plans P et Q sont parallèles.

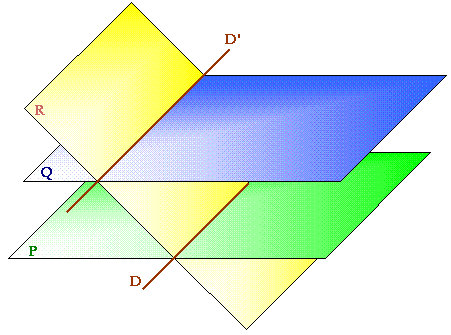
L'intersection des plans P et R est la droite D. De même, D' est l'intersections de Q et R. Comme les plans P et Q sont parallèles alors les droites D et D' le sont aussi.

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Décembre 1998/Janvier 2003. Tous droits réservés.