

La preuve :
 Soit M un point de la droite (AB) distinct
de A et de B. On appelle M’ son image par l’homothétie h. Comme
A, B et M sont alignés, il en va alors de même pour les points A’, B’ et M’. Grâce au théorème
2.1. Donc M’
Soit M un point de la droite (AB) distinct
de A et de B. On appelle M’ son image par l’homothétie h. Comme
A, B et M sont alignés, il en va alors de même pour les points A’, B’ et M’. Grâce au théorème
2.1. Donc M’ (A’B’).
(A’B’).
On a donc montré que tout point de la droite (AB) avait pour
image un point de la droite (A’B’). En clair, nous venons de prouver que
h( (AB) ) Ì (A’B’).
Note : h( (AB) ) désigne l’image de la
droite (AB) par l’homothétie h.
Il reste donc à monter que (A’B’) Ì
h( (AB) ), c’est-à-dire que tout point de la droite (A’B’) est l’image
par h d’un point de la droite (AB).
 Soit N’ un point de la droite (A’B’).
Les points A’, B’ et N’ sont donc alignés. Il existe donc un unique
réel a tel que
Soit N’ un point de la droite (A’B’).
Les points A’, B’ et N’ sont donc alignés. Il existe donc un unique
réel a tel que ![]() .
.
On appelle N le point de la droite (AB) défini par ![]() .
Il est clair que les points A, B et N sont alignés. Donc N
.
Il est clair que les points A, B et N sont alignés. Donc N (AB).
(AB).
Nous allons montrer que N est l’antécédent par h du point
N’.
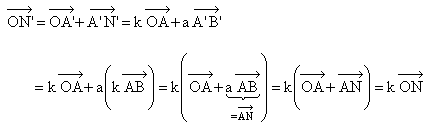
Donc N’ est l’image par h de N qui est un point de (AB). Mission accomplie !
Ainsi l’image par h de la droite (AB) est-elle la droite (A’B’) !
 La dernière chose à voir
est que les droites (AB) et (A’B’) sont parallèles.
La dernière chose à voir
est que les droites (AB) et (A’B’) sont parallèles.
D’après le théorème 1.3, on
sait que les vecteurs ![]() sont
colinéaires. Or l’un et l’autre sont des vecteurs directeurs respectifs
des droites (A’B’) et (AB). Cela nous assure que ces deux dernières
soient parallèles.
sont
colinéaires. Or l’un et l’autre sont des vecteurs directeurs respectifs
des droites (A’B’) et (AB). Cela nous assure que ces deux dernières
soient parallèles.