1°) Quelques mots d'introduction sur nos amis les vecteurs.
La notion de vecteur n'est pas nouvelle. Elle a été vue en troisième. Rappelons d'abord ce qu'est un vecteur.
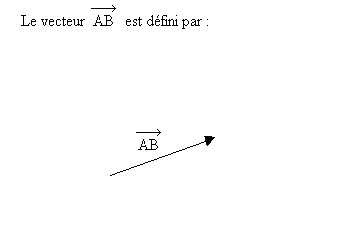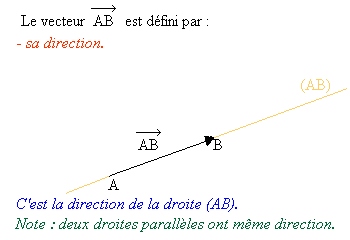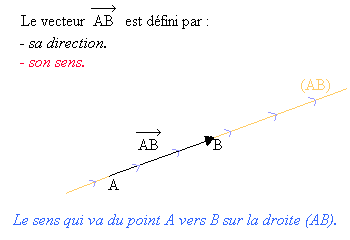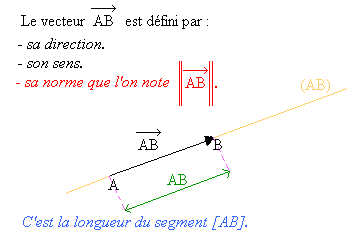
Un vecteur se définit de la manière suivante :
Autre rappel : l'égalité de deux vecteurs. A l'instar des nombres, deux vecteurs 
peuvent être égaux. Quatre possibilités permettent de dire qu'ils le sont. C'est ce que résume l'animation suivante :
Si deux vecteurs sont égaux, on dit qu'ils sont les représentants d'un même vecteur. Ce vecteur ne dépend ni de A, ni de B, ni de C, ni de D. Il ne dépend d'aucun point.
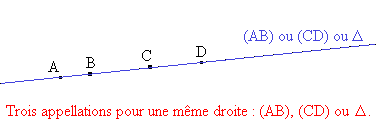
Une droite peut être désignée par deux de ses points (par exemple, la droite (AB) ou encore (CD) ) ou 'encore par un nom qu'on lui donne (par exemple 
). Comme sur la figure suivante :
, on peut désigner ce vecteur de manière indépendante de points particuliers. Au lieu de l'appeler , on peut l'appeler par exemple 
. Ainsi a-t-on que 
.
Une question se pose : si A est un point, qu'est le vecteur 
?
Analysons ce vecteur :
sa direction : c'est la direction de la droite (AA) ! Autrement dit la direction d'une droite qui n'existe pas. Ce vecteur n'a donc pas de direction.
son sens : ce vecteur n'ayant pas de direction, il ne peut avoir de sens !
sa norme : la norme du vecteur est égale à la longueur AA, c'est-à-dire à 0.
En fait, est le représentant d'un vecteur qu'on appelle le vecteur nul et qu'on note 
. Ce vecteur nul n'a ni direction, ni sens. Par contre, sa une norme (ou sa longueur) est égale à 0.