D et
sont deux droites non parallèles. M est un point quelconque du plan.
La question : construire le point M’ image du point M par la projection sur la droite D parallèlement à
(ou d’axe ).6°) Dernières missions : théorèmes de projection et de Thales.
Vous connaissiez le théorème de Thales depuis la quatrième. Vous en découvrirez une nouvelle variante à la fin de ce paragraphe !
Projection sur une droite parallèlement à une autre.
Vous connaissiez déjà la projection orthogonale sur une droite particulière. Vous connaissiez donc un membre de la famille que nous allons aborder de suite.
D et sont deux droites non parallèles. M est un point quelconque du plan.
La question : construire le point M’ image du point M par la projection sur la droite D parallèlement à (ou d’axe ).
En résumé, nous avons la configuration suivante :
En définitive, le point M’ est donc le point d’intersection de la droite D avec la parallèle à passant par M.
Quelques remarques :
Si ’ est une parallèle à alors que peut-on dire de la projection sur la droite D parallèlement à ?.
Réponse : c’est la même que la projection sur D parallèlement sur .
Pour construire l'image M" du point M par la projection sur (D) parallèlement à ('), on trace la parallèle 'M à (') passant par M.
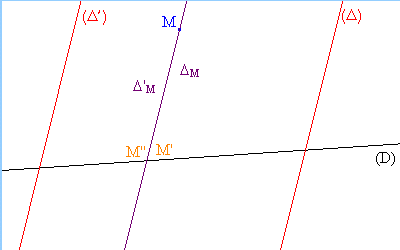
passant par M. Par conséquent, le point M" sera confondu avec le point M'.
La projection orthogonale est une forme particulière de projection sur un axe parallèlemement à un autre. Toute perpendiculaire à D peut servir d’axe à cette projection.
Maintenant que nous savons ce qu’est une projection parallèment à une droite, intéressons-nous à un gros morçeau : le théorème de projection.
Le théorème de projection ressemble à s'y méprendre une partie du théorème de Thales. En fait, le premier sert à montrer le second !
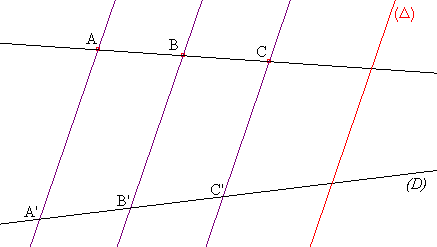
La démonstration de ce théorème est hors programme. Mais elle est disponible.
La première écriture rencontrée de ce théorème est celle d'un rapport de longueurs. La seconde est vectorielle.
La preuve :
Nous avons deux points à montrer. Pour le second, nous emploierons notre théorème de projection et montrerons ainsi que point inutile il n'est !
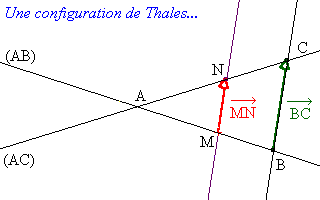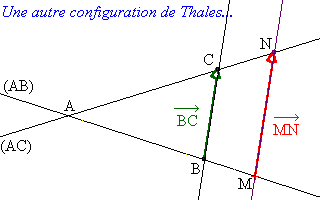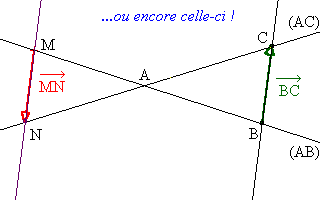
(i) : On suppose ici que 
.
On peut alors écrire que :
. Ce qui en application du théorème 5.4 nous permet d'ajouter que les droites (MN) et (BC) sont parallèles.
(ii) : On suppose à présent que 
et que (MN) est parallèle à (BC).
Faisons une figure
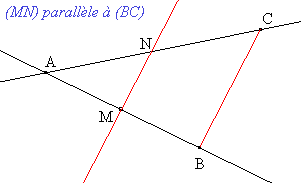
| A a pour image A, |
| M a pour image N car (MN) est parallèle à (BC), |
| B a pour image C. |
, en application du théorème de projection, il vient que 
.