1°) Colinéarité et coordonnées.
Il existe un test sur les coordonnées permettant de dire quand est-ce que deux vecteurs sont colinéaires. Ce test est incarné par le théorème suivant.
La démonstration de ce théorème n'est souvent jamais traitée en cours. Pour y accéder, utiliser le bouton ci-dessous.
Une remarque : le déterminant de deux vecteurs.
La différence des produits x.y' - x'.y est appelée déterminant des vecteurs 
et 
. On le note det( , ). En règle générale, retenez que :
Une des conséquences de ce théorème est que deux vecteurs non nuls sont colinéaires si et seulement si leur déterminant est non nul.
En effet si et , seule demeure dans le théorème la condition 
. Ce qui équivaut à dire que ces deux vecteurs sont colinéaires.
Applette déterminant si deux vecteurs sont-ils colinéaires ?
Jusqu’à présent les seules équations de droite que vous connaissiez étaient de deux formes :
Le théorème vu au premier paragraphe va nous aider à répondre à la question. Voyons ce qu'il devient lorsque le vecteur est nul.
En effet, seule demeure la possibilité .
Equation d'une première droite.
Intéressons-nous à la droite D qui passe par le point A(2 ; 3) et dont le vecteur (-1 ; 4) est l'un des vecteurs directeurs.
Une droite est parfaitement défini par un vecteur qui lui donne sa direction et un point par lequel elle passe.
Si le point M a pour coordonnées (x ; y) alors 
(x – 2 ; y – 3).
De même, dire que le point M fait partie de la droite D équivaut à dire qu'il existe un réel k tel que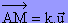 
. Ceci car est un vecteur directeur de D.
Exploitons cette remarque avec l'aide de notre proposition. Le vecteur y jouera le rôle de . Le de la proposition sera le vecteur .
Autrement tout point M(x ; y) de la droite D vérifie l'équation 4.x + y –11 = 0.
Réciproquement l'ensemble des points M(x ; y) vérifiant 4.x + y –11 = 0 est la droite passant par A et dont est l'un des vecteurs directeurs.
On dit que 4.x + y –11 = 0 est une équation cartésienne de la droite D. Je dis une car il y en a plusieurs.
L'équation 8.x + 2.y – 22 = 0 est en une autre.
Mais au lieu de nous arrêter là, nous aurions pu aller plus loin. Nous serions alors retomber sur l'équation réduite de la droite D.
y = -4.x + 11 est l'équation réduite de la droite D. A la différence des équations cartésiennes, elle est unique. Celle-ci est de la forme y = m.x + p. Le coefficient directeur m de D vaut –4.
Equation d'une seconde droite.
Maintenant considérons la droite D' qui passe par les points A(3 ; -2) et B(3 ; 5).
Ceux qui se rappellent leur cours de Troisième diront qu'étant donné que ces points ont même abscisse, l'équation de la droite D' est x = 3.
D'accord mais pourquoi ?
Le vecteur 
(0 ; 7) est un vecteur directeur de D'. Le raisonnement fait pour la droite D reste encore valable. Le vecteur a pour coordonnées (x – 3 ; y + 2). Ainsi :
7x – 21 = 0 est donc une équation cartésienne de D'.
x – 3 = 0 en est une autre.
Comme pour D, on peut aller un peu plus loin.
L'équation réduite de la droite D' est x = 3. Elle est de la forme x = q.
Généralisation de ces deux raisonnements.
Ce que nous avons vu pour deux droites se généralise à toutes au travers du théorème suivant :
Par exemple, pour la première droite D, a = 4, b = 1 et c = -11.
Pour la seconde droite D', a = 7, b = 0 et c = -21.
La démonstration de ce théorème est la généralisation des deux cas particuliers que nous avons traités. Pour y accéder, utiliser le bouton ci-desssous.
Notes et remarques :
En résumé, toute droite D admet une équation de la forme a.x + b.y + c = 0.
On dit que a.x + b.y + c = 0 est une équation cartésienne de la droite. Une car une droite a une multitude d’équations cartésiennes.
Une équation de la forme y = m.x + p ou x = p est l’équation réduite de la droite. La car elle n’en admet qu’une seule.
Une droite peut avoir plusieurs équations cartésiennes.
Pour savoir si deux équations cartésiennes sont celles d'une même droite, cliquer ici.
Applette détermination une équation cartésienne d'une droite.
Pour déterminer une équation cartésienne d'une certaine droite, il suffit de faire comme dans les deux exemples.
Un vecteur directeur bien particulier.
Trouver un vecteur directeur d’une droite n’est à priori pas chose facile. Pourtant...
Par exemple si D a pour équation 3x - 2y + 5 = 0 alors le vecteur (2 ; 3) est un vecteur directeur de D.
La preuve de la proposition :
Le point A(xA ; yA) est un point de la droite D (on le choisit comme tel). Les coordonnées de A vérifient donc l'équation de la droite D. Ainsi a.xA + b.yA +c = 0.
On définit le point B par = . Le point B a alors pour coordonnées (xA – b ; yA + a).
Regardons si B fait partie de la droite. On regarde donc si ses coordonnées vérifient l'équation de cette dernière.
est donc un vecteur directeur de D. Or le vecteur est aussi le vecteur .
Le vecteur (-b ; a) est donc l'un des vecteurs directeurs de la droite D.
Comment tracer une droite dont on ne connaît qu'une équation cartésienne ?
C'est une grande question ! Et pourtant, la réponse y est fort simple !
Intéressons-nous par exemple à la droite D d'équation : x - 2y + 3 = 0.
Pour tracer une droite, il suffit de connaître deux de ses points et d'utiliser la règle.
Les points A(1 ; 2) et B(3 ; 3) sont deux points de D. En effet leurs coordonnées en vérifient l'équation cartésienne.
Le plus "dur", c'est de trouver deux points. Le reste n'est plus que du dessin...
3°) Condition de parallélisme de deux droites.
Nous avons vu une condition sur les coordonnées de deux vecteurs pour qu’ils soient colinéaires, nous allons en énoncer une autre pour les droites. Cette fois, on ne parlera plus de coordonnées mais d’équations cartésiennes, on ne parlera plus de colinéairité mais de parallélisme.
Applette déterminant si deux droites sont parallèles.
La preuve de ce théorème :
D est la droite d'équation a.x + b.y + c = 0 donc le vecteur (-b ; a) est l'un des vecteurs directeurs de cette droite.D' est la droite d'équation a'.x + b'.y + c' = 0 donc le vecteur (-b' ; a') est l'un des vecteurs directeurs de celle-ci.
Ce qui démontre ce théorème.
Conséquence sur le coefficient directeur.
La conséquence de ce théorème est une chose qui a été vue en troisième.
D et D' sont deux droites dont les équations réduites respectives sont y = m.x + p et y = m'.x + p'.
Sachant cela, on peut dire que :
m.x – y + p = 0 est une équation cartésienne de la droite D.
m'.x – y + p' = 0 est une équation cartésienne de la droite D'.
Le théorème vu précédemment nous permet alors d'écrire :
Autrement dit ce que nous savions déjà : dire que deux droites non parallèles à l'axe des ordonnées sont parallèles entre elles équivaut à dire qu'elles ont même coefficient directeur.