Chacun à présent est sensé savoir que l’ensemble des points M(x;y) vérifiant l’équation a.x + b.y + c = 0 est une droite.
Chacun sait qu’un système du type
peut n’avoir aucune solution, une seule ou bien alors une infinité.
Nous connaissons déjà le déterminant de deux vecteurs. On définit aussi le déterminant d’un système.
Quelques remarques :
Si S est le nom du système alors son déterminant peut s’écrire det(S).
Le déterminant est aussi noté sous la forme :
Le critère suivant permet d’en savoir plus long sur le nombre de solutions d’un système....
Une remarque sur le théorème :
Pourquoi impose-t-on que a et b ne soient pas tous les deux nuls ?
Imaginons qu’ils le soient. A ce moment là, la première équation deviendrait 0 = c. Ce qui franchement n’a d’intérêt que pour qui ne veut pas se crever...
Il en va de même pour a’ et b’.
La preuve de ce théorème :
L’ensemble des points M(x ; y) vérifiant l’équation a.x + b.y - c = 0 est une droite que nous appellerons D.
Celui des points M(x ; y) vérifiant a’.x + b’.y - c’ = 0 est une autre droite D’.
Chaque solution (x ; y) du système est les coordonnées d’un point d’intersection de D et D’. En fait l’un est l’autre sont intimement liés à tel point qu’on peut se poser des questions.
Dans le plan, deux droites sont soit parallèles ou confondues ou bien encore sécantes
Or nous avons vu que :
Si 
alors les droites D et D’ sont parallèles (ou confondues).
Si elles sont parallèles non confondues, elles n’ont aucun point d’intersection. A ce moment, le système n’admet aucune solution.
Si D et D’ sont confondues alors tout point de l’une est un point de l’autre. Elles ont donc une infinité de points d’intersection. Le système admet donc une infinité de solution.
Si 
alors D et D’ sont sécantes. Elles n’ont qu’un seul point d’intersection, ce qui explique l’unicité de la solution du système.
D’où notre théorème !
Quelques remarques :
L’intérêt du déterminant est qu’il permet de bien orienter les calculs dés le début. Avant, on se lançait un peu à l’aventure. A présent, on est un peu mieux renseigner sur la démarche à tenir.
La notion de déterminant n’est pas du programme de Seconde... Mais nous, on s’en fout !
La résolution d’une équation se fait dans 
. Celle d’un système, se fait dans 2 qui est l’ensemble de tous les couples de réels (x ; y). Chaque point du plan étant repéré par un unique couple (x ; y), on identifie (souvent) 2 au plan...
Nous avons vu la théorie avec ce déterminant. Au travers de ce paragraphe, nous allons nous intéresser à la résolution effective des systèmes avec deux méthodes maîtres : par substitution et par combinaisons linéaires.
Résolvons dans 2 le système :
On commence par prendre de bonnes habitudes. On calcule le déterminant de ce système.
Le déterminant du système étant nul, il admet soit aucune solution, soit une infinité.
S’il en admet une infinité, c’est qu’en fait les droites D : 3.x - 7.y - 2 = 0 et D’ : -1,5 × x + 3,5 × y + 1 = sont confondues.
Autrement dit, tout point de l’une est point de l’autre !
On choisit donc un point de D. Par exemple le point M( 2/3 ; 0). Voyons si ses coordonnées vérifient l’équation de D’.
Donc il fait bien partie de D’. Le couple (2/3 ; 0) est donc solution du système.
Par conséquent, le système ne peut admettre qu’une infinité de solutions. On conclut la résolution en disant que :
"L’ensemble des solutions du système est l’ensemble des couples de réels (x ; y) vérifiant 3.x - 7.y -2 =0 " .
Sous forme symbolique, cela se note :
S = { (x ; y)Î
2 tels que 3.x -7.y - 2 = 0}
A noter qu’on aurait pu conclure en disant qu’il s’agissait des couples (x ; y) vérifiant l’équation -1,5 × x + 3,5 × y +1 = 0.
En effet ces deux équations sont équivalentes. Dans le plan, ce sont deux équations cartésiennes d’une même droite.
Résolvons dans 2 le système :
Nous connaissons déjà le déterminant de ce système (voir le cas précédent). Il est nul. Donc il y a soit une infinité de solution, soit aucune.
S’il en admet une infinité alors toute solution de la première équation est solution de la seconde.
Le couple de réels (-7/3 ; 0) est une solution de la première équation. Voyons s’il est solution de la seconde. Comme précédemment...
(-7/3 ; 0) n’est donc pas solution de la seconde solution. Par conséquent, les droites D et D’ sont parallèles mais non confondues. Elles n’ont aucun point d’intersection. Le système n’admet aucune solution.
Symboliquement, la conclusion se note :
S = Æ .
Résolvons dans 2 le système :
Avant toute résolution, on commence par calculer le déterminant de ce système.
Le déterminant étant non nul, le système admettra donc une et une seule solution.
La résolution peut se faire de deux manières : par substitution ou par combinaisons linéaires. Nous verrons ces deux méthodes.
On cherche à exprimer dans une des deux équations une inconnue en fonction de l’autre. Dans la première équation, on choisit d’exprimer y en fonction de x. Il vient donc :
Dans la seconde équation, on remplace y par son expression en x. La seconde équation devient alors une équation du premier degré en x…que nous savons résoudre.
Pour avoir la valeur de y, il suffit de remplacer x par la sienne dans l’expression en fonction de x que nous avons obtenue. Ainsi :
Pour conclure, nous écrirons donc que :
.
Résolution par combinaisons linéaires.
Nous allons résoudre par combinaisons linéaires le système
Par combinaisons linéaires, cela signifie que nous allons faire des sommes de produits afin d’éliminer l’une des deux inconnues.
On décide de supprimer y. On multiplie la première par 3 et la seconde par 2. Puis on les ajoutera membre à membre.
Puis on les ajoute membre à membre :
d’où
Pour déterminer y, on remplace x par sa valeur dans une des deux équations du système : la première par exemple.
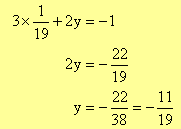
L’unique solution de ce système est le couple (1/19 ; -11/19). Ce que l’on résume par :
Une remarque :
Aucune de ces deux méthodes n’est meilleure que l’autre. Selon les circonstances et les individus, elles sont plus ou moins commodes à utiliser…
3°) L'applette résolvant les systèmes.
Vous n'avez pas envie de résoudre vos systèmes 2x2 ? Ca tombe bien car ce paragraphe le fait pour vous. Et dans le détail s'il vous plait !
La résolution peut se faire au choix soit par substitution, soit par combinaison linéaires.
Le système est :
4°) Résolutions d'autres systèmes.
Résolution de systèmes non linéaires.
Certains systèmes non linéaires peuvent être résolus comme s'ils l'étaient (linéaires). Illustration avec l'exemple qui suit :
Avant toute chose, résolvons le système linéaire correspondant d'inconnues (u ; v) qui est :
On montre (par une résolution) que l'unique solution de ce système est le couple (4 ; 5).
Revenons à présent à ce système :
Autrement dit, pour qu'un couple (x ; y) soit solution de notre système, il faut et il suffit que x vaille –2 ou 2, et que y soit égal à –5 ou 5. Il ne reste plus qu'à énoncer tous les couples solutions.
S = {(-2 ; -5), (-2 ; 5), (2 ; -5), (2 ; 5)}
En clair, l'ensemble des solutions est l'ensemble formé par les couples (-2 ; -5), (-2 ; 5), (2 ; -5) et (2 ; 5).
Résolution d'un système à trois équations et trois inconnues.
On peut corser la difficulté en passant d'un système 2 × 2 à un système de trois équations à trois équations. Illustration avec ce qui suit !
Comme pour les systèmes à deux équations, on peut en connaître le nombre de solutions en calculant le déterminant. Mais c'est (largement) hors programme !
Ce système peut être résolu de deux manières :
par substitution : à partir de la première équation, on exprime par exemple x en fonction de y de z. En remplaçant x par ce qui a été trouvé dans les deux dernières équations, on retombe alors sur un système à deux équations dont les inconnues sont y et z.
par combinaisons linéaires. C'est comme cela que nous allons procéder.
Le but de la manœuvre est de se ramener à un système de deux équations à deux inconnues. On décide de conserver x et z. Il s'agit donc d'éliminer y par une série de combinaisons linéaires.
Cette résolution peut se faire soit par combinaisons linéaires, soit par substitution. On trouve que x = 1 et z = 2. Pour obtenir y, on remplace x et z par leurs valeurs dans la seconde équation par exemple.
La résolution graphique d'un système à trois inconnues se fait dans l'espace (trois dimensions, une par inconnue). L'ensemble des solutions est soit le vide, soit un point, une droite ou bien encore un plan...