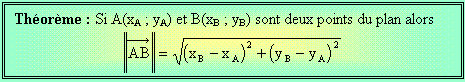
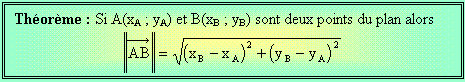
La preuve de ce théorème :
Nous savons (c’est glissant) que le vecteur ![]() a pour coordonnées (xB - xA ; yB - yA).
a pour coordonnées (xB - xA ; yB - yA).
On appelle C le point de coordonnées (xB ; yA).

On peut alors écrire que :
![]() = (xB - xA).
= (xB - xA).![]()
A et C sont donc deux points de la droite dont D dont ![]() est un vecteur directeur et qui passe par A. Dans le repère de cette droite qu'est (A ;
est un vecteur directeur et qui passe par A. Dans le repère de cette droite qu'est (A ;![]() ), on peut écrire que :
), on peut écrire que :

De la même manière :
![]() = (yA - yB).
= (yA - yB).![]()
A et B sont donc deux points de la droite dont D' qui passe par B et dont ![]() est un vecteur directeur. Dans le repère de cette droite qu'est (B ;
est un vecteur directeur. Dans le repère de cette droite qu'est (B ;![]() ), on peut écrire que :
), on peut écrire que :

De plus, la droite D est parallèle à (OI). En effet ![]() est un vecteur directeur de ces deux droites.
est un vecteur directeur de ces deux droites.
Il en va de même pour D' et (OJ). Comme (OI) est perpendiculaire à (OJ), les droites D et D' sont donc elles-aussi perpendiculaires.
C étant le point d'intersection de ces deux droites, le triangle (ABC) est donc rectangle en C. Le théorème de Pythogore lui est donc applicable. Ainsi :
AB2 = AC2 + BC2
Ainsi donc :

Autrement dit :

En définitive, nous pouvons dire que nous avons gagné !
Note : certains diront peut-être que cette démonstration est une escroquerie. En effet le point C peut être confondu avec A ou B. Il suffit pour cela que A et B aient même ordonnée ou même abscisse. Le triangle (ABC) est alors plat, C étant confondu avec A ou B. Comment peut-on alors parler de triangle rectangle ? En fait, il n'y a aucun problème car le théorème de Pythagore marche parfaitement pour ces cas-là...