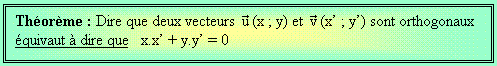
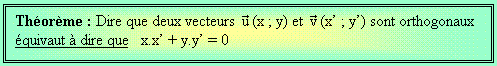
Preuve du théorème établissant une condition d’orthogonalité entre deux vecteurs :
Nous allons montrer par équivalence que deux vecteurs 
(x ; y) et 
(x’ ; y’) sont orthogonaux si et seulement si x.x’ + y.y’ = 0..
Mais avant d’entamer les opérations de démonstration, préparons le terrain!
On appelle A le point du plan défini par 
= . Le point A a alors pour coordonnées (x ; y).
On appelle B le point du plan défini par 
= . Le point B a alors pour coordonnées (x’ ; y’).
On s’intéresse à présent aux distances AB, OA et OB. Comme le repère (O ; 
, 
) est orthonormal (on dit aussi orthonormé) alors :
Ces préliminaires effectués, nous disposons de tous les outils nécessaires pour démontrer notre théorème.
Autrement dit, ce qu’on voulait! Ainsi le théorème est-il démontré!
Note : le théorème de Pythagore marche même lorsque O est confondu avec A et B... Certains objecteront peut-être que c'est un abus de langage : comment peut-on parler de perpendicularité entre une droite et un point ?Dans ce que nous avons fait, une seule chose est litigieuse : "(OA) et (OB) orthogonales". Il faudrait dire "(OA) et (OB) orthogonales ou A confondu avec O ou B confondu avec O". Ce serait pédagogiquement plus correct...