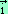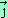, 
). I et J sont deux points définis par :
Note : dans tout ce qui suit, on suppose le plan muni d’un repère orthonormé (O ; 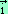, 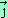). I et J sont deux points définis par :
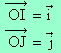
1°) Quelques choses essentielles au reste...
Chacun connaît l’orthogonalité des droites. On définit également l’égalité de deux vecteurs non nuls.
Par convention, le vecteur nul (qui n’a pas de direction) est orthogonal à tous les vecteurs du plan.
Si deux vecteurs 
et 
sont orthogonaux, on écrit alors que ^ .
Norme d’un vecteur dans un repère orthonormé.
Rappelons pour commencer une chose qui est déjà connue.
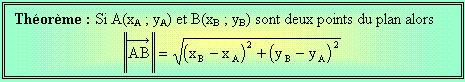
La démonstration de ce théorème repose sur le théorème de Pythagore. Pour y accéder, utiliser le bouton ci-dessous.
Par exemple, si A(2 ; 4) et B(3 ; -2) alors
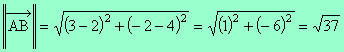
Nous connaissons désormais l’expression de la norme d’un " vecteur à points ". Mais qu’en est-il pour un vecteur (x ; y) ?
Appelons M le point défini par 
= . Les coordonnées du point M sont donc (x ; y).
Ces vecteurs étant égaux, ils ont même normes. Or la norme du vecteur 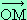, nous la connaissons ! Tout du moins, nous pouvons la connaître. En effet :
A partir de là, nous disposons de tous les éléments pour répondre à notre question par la proposition suivante.
Par exemple, si (-3 ; 4) alors
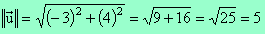
Note importante : Cela n’est valable que dans un repère orthonormé ! Autrement, c’est une autre formule qui en ce qui nous concerne est hors programme.
2°) Condition d’orthogonalité de deux vecteurs et conséquences.
Condition d’orthogonalité de deux vecteurs.
A l’instar de la colinéarité, il existe un " test" permettant de dire à partir de leurs coordonnées si deux vecteurs sont orthogonaux ou pas...
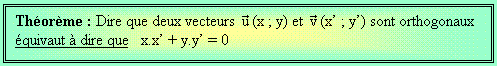
La démonstration de ce théorème repose sur le théorème de Pythagore ainsi que sur la norme d'un vecteur. Pour y accéder, utiliser le bouton ci-dessous.
Note importante : ce théorème ne s’applique que dans le cas où le repère est orthonormé.
|
Applette déterminant si deux vecteurs sont orthogonaux.
|
Conséquences sur la perpendicularité de deux droites.
Comme un bonheur ne vient jamais seul, cette condition vectorielle déteint sur la perpendicularité de deux droites...
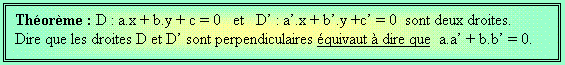
Note importante : comme pour les vecteurs, ce théorème de s’applique que dans le cas où le repère est orthonormé.
|
Applette déterminant si deux droites sont perpendiculaires. |
La preuve de ce théorème :
D ayant pour équation a.x + b.y + c = 0 alors le vecteur (-b ; a) est un vecteur directeur de D. Et donc et D ont même direction.
De même le vecteur (-b’ ; a’) est un vecteur directeur de la droite D’. Les deux comparses ont donc même direction.
Pour arriver à nos fins, nous allons procéder par équivalence.
et sont orthogonaux.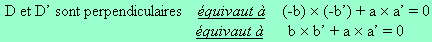
Autrement dit, ce que l’on voulait !
En Troisième, on voit une condition d’orthogonalité portant sur les coefficients directeurs. En fait, cette condition est un cas particulier de notre théorème.
Si l’équation réduite de la droite D est y = m.x + p alors une équation cartésienne de celle-ci est :
En application du théorème, il vient donc que :
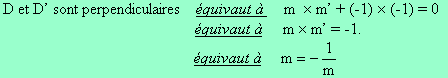
Cela nous permet d’établir le corollaire suivant :
Qu’est-ce qu’un corollaire ?
Un corollaire est la conséquence d’un théorème. Mais celle-ci est tellement importante qu’on décide de la "sacraliser". On n'en fait pas un théorème mais un corollaire. Le corollaire précédent découle du théorème situé avant.
Le vecteur normal d’une droite est à l’orthogonalité ce qu’est le vecteur directeur à la colinéarité.
La conséquence de cette définition est la proposition suivante :
En effet, si est un vecteur normal à D alors la direction de est perpendiculaire à celle de D qui est celle du vecteur . Et réciproquement !
De même, si est un vecteur normal à D alors toute droite dont est un vecteur directeur est perpendiculaire à D.
De même si et sont deux vecteurs normaux à la droite D alors et sont colinéaires entre eux.
Certains me diront : les vecteurs normaux, c’est bien beau mais si on ne peut pas en trouver simplement alors ça sert à rien ! Et ils ont raison ! Mais le théorème suivant va répondre à leur attente.
Par exemple si D a pour équation 3x - 2y + 5 = 0 alors le vecteur (3 ; -2) est un vecteur normal de D. Il est orthogonal au vecteur directeur qu'est (2 ; 3).
La preuve de ce théorème :
Si la droite D a pour équation a.x + b.y + c = 0 alors un vecteur directeur de D est le vecteur (-b ; a).
Faisons un test d’orthogonalité sur le vecteur et le vecteur .
et sont orthogonaux. En application de la précédente proposition, il vient alors que (a ; b) est un vecteur normal de D.
Le vecteur normal est important dans la mesure où il permet de déterminer l’équation cartésienne d’une droite en ne connaissant qu’un point de celle-ci et l’un de ses vecteurs normaux.
Illustration de l'utilité du vecteur normal pour une équation de droite.
Déterminons une équation cartésienne de la droite D dont l’un des vecteurs normaux est le vecteur (a ; b) et qui passe par le point A(xA ; yA).
Avant toute chose, nous remarquons que :
si M est un point de D distinct de A alors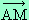 
est un vecteur directeur de D. En vertu de la proposition précédente, lui et sont donc orthogonaux.
Si M est confondu avec A alors le vecteur 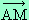est nul. Il est donc orthogonal à .
Réciproquement, si M est un point tel que 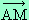et sont orthogonaux alors de deux choses l’une :
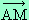soit le vecteur est nul et à ce moment-là, A et confondu avec M. Donc MÎD.
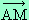soit le vecteur est non nul. Alors c’est nécessairement un vecteur directeur de la droite D. Autrement dit, MÎD.
Nous venons donc de montrer que :
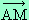et sont orthogonaux.La percée est faite ! Exploitons-la.
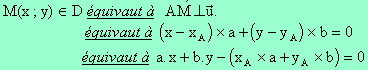
La question qui peut se poser est : à quoi tout cela sert-il ?
En fait, nous venons de déterminer une équation cartésienne de la droite D à partir d'un de ses points et de l'un de ses vecteurs normaux! L'applette qui suit généralise ce raisonnement.
|
Applette déterminant une équation cartésienne de droite à partir d'un vecteur normal. Pour déterminer une équation cartésienne d'une certaine droite, il suffit de faire dans un cas particulier ce que nous venons de faire en général. |