Jusqu'à présent, tous les repères abordés étaient définis par trois points. Le plus souvent ils s'appelaient O, I et J. A présent, nous définirons ceux-ci avec un point et deux vecteurs introduisant par là-même la notion de base.
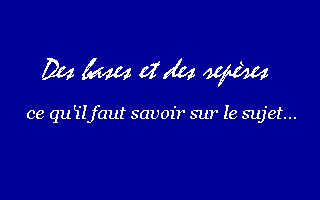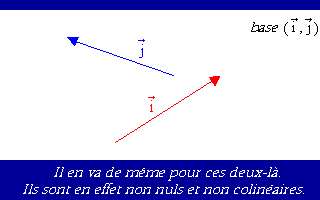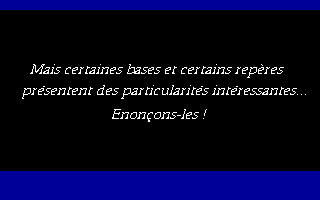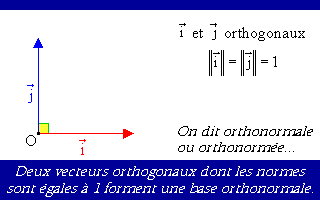
Un repère peut alors être défini comme un duo formé d'un point et d'une base.
Le point O est appelé origine du repère. Le couple (
, 
) est la base associée à ce repère.
Sans compter qu'il y a des repères particuliers :
Ce qui change par rapport à la Troisième :
Avant un repère était défini par trois points. Maintenant il l'est par un point et deux vecteurs. On pourrait croire que cela change beaucoup de choses en fait cela ne change rien.
En effet si l'on pose
alors le repère (O; , ) est aussi le repère (O, I, J).
2°) Coordonnées d’un point dans un repère.
Pour tout le paragraphe, on munit le plan d’un repère quelconque (non donc particulier) (O; , ).
Notre but : dire ce que sont les coordonnées d’un point dans un repère.
Coordonnées d’un point : la construction.
Si vous souhaitez en savoir plus sur la démonstration de ce théorème, utilisez le bouton ci-dessous !
Quelques remarques :
Si M a pour coordonnées le couple (x ; y), on dit alors que x est l’abscisse du point M alors que y en est l’ordonnée.
Les coordonnées d’un point dépendent du repère dans lequel on se trouve.
"M a pour coordonnées (x ; y) dans la base (O;,)" se note de deux manières :
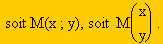
Applette illustrant les coordonnées d'un point dans un repère.
Mode d'emploi :
Les points et vecteurs sont déplaçables. Il suffit de cliquer et de les bouger à l'endroit voulu tout en maintenant le bouton de la souris enfoncé. Le mieux, c'est encore de voir par vous-même...
Coordonnées du milieu d’un segment.
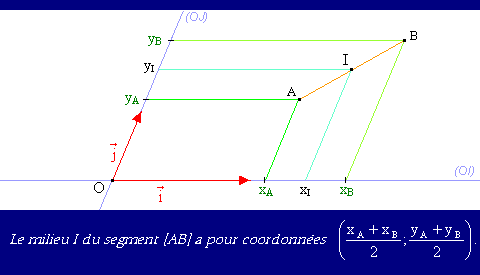
La preuve de ce théorème :
Pour arriver à nos fins, nous allons utiliser un théorème que nous avions vu à l’occasion de la caractérisation vectorielle des milieux.
Comme I est le milieu de [AB] alors 
. Ce qui s’écrit encore :
,).
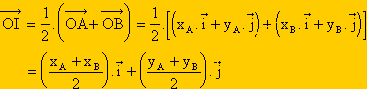
3°) Coordonnées d’un vecteur et conséquences.
Dans tout le paragraphe, on munit le plan d’un repère quelconque (O, ,). Ce qui induit que les vecteurs et ne sont pas colinéaires. Ils sont encore moins nuls.
Nous allons définir ce que sont les coordonnées d’un vecteur dans le repère (O, , ).
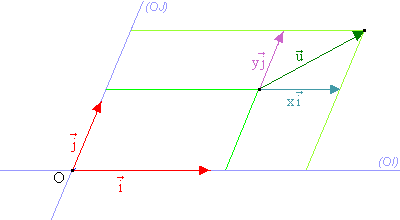
Si vous souhaitez en savoir plus sur la démonstration de ce théorème, utilisez le bouton ci-dessous.
Quelques remarques :
Comme pour les points, on dit que x est l’abscisse du vecteur 
alors que y en est l’ordonnée.
Les coordonnées d’un vecteur dépendent de la base (couple de vecteurs ( , ) non colinéaires) dans laquelle on se trouve.
" a pour coordonnées (x ; y) dans la base ( , )" se note de deux manières :
Certains vont me dire, les coordonnées c’est bien beau ! Mais si deux vecteurs sont égaux, ils doivent nécessairement avoir même coordonnées. C’est logique !
Oui c’est logique et c’est d’ailleurs le cas !
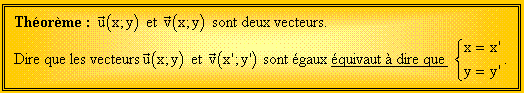
Cela parait logique, mais nous allons quand même le montrer !
La preuve du théorème :
Une équivalence, c’est deux implications. La démonstration du théorème requiert donc que nous prouvions successivement que :
Entamons les hostilités :
(i) Si = 
alors ils ont même coordonnées. Ou plutôt les coordonnées de l’un sont les coordonnées de l’autre. Ainsi vient-il que
Réciproquement :
(ii) Supposons que x = x’ et y = y’.
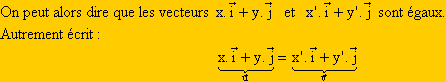
Ainsi les vecteurs (x ; y) et (x' ; y') sont-ils égaux. Ce qui quelque part est quand même rassurant !
Coordonnées de vecteur, addition vectorielle et produit par un réel.
L’avantage des coordonnées, c’est qu’elles laissent tout passer : de vraies carpettes !
De modestes preuves de ce modeste théorème :
L’énoncé comportant deux points, la démo comportera donc deux points.
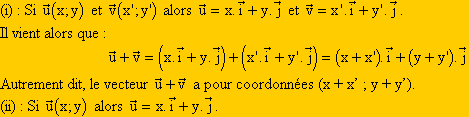
Il vient alors que :
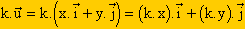
Autrement dit, le vecteur k. a pour coordonnées (k.x ; k.y).
Lien entre coordonnées d’un vecteur et celles d’un point.
Les coordonnées d’un vecteur 
peuvent s’exprimer en fonction des celles de A et de celles de B. La preuve (après la proposition...)
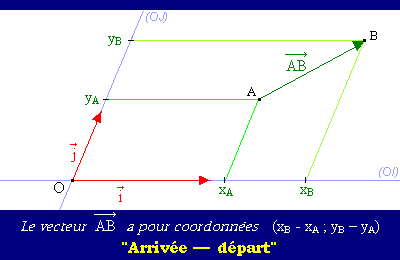
La preuve :
En effet, si A et B ont pour coordonnées respectives (xA ; yA) et (xB ; yB) alors
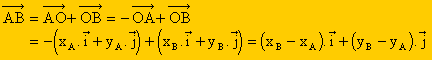
sont-elles (xB - xA ; yB - yA ).
4°) Coordonnées d'un point défini par une égalité vectorielle.
Dans ce dernier paragraphe, nous allons mettre en oeuvre concrètement au travers d'un exercice toutes les propriétés que nous venons de voir.
L'exercice :
.
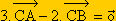Cet exercice peut être résolue de plusieurs d'entre elles. Voici deux d'entre elles :
Deux réponses possibles:
Dans ce qui suit, le couple (xC ; yC) désigne les coordonnées du point C que nous cherchons.
Deux cheminements sont possibles.
1ère solution. La plus simple : on cherche à réduire cette relation vectorielle. On va chercher à exprimer 
en fonction de 
. On utilise ainsi un peu de géométrie vectorielle avant de rentrer dans la géométrie analytique.
La relation de Chasles nous permet de simplifier la relation vectorielle. Ainsi :
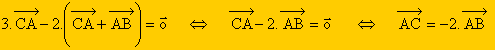
a pour coordonnées (xC + 2 ; yC – 5).
(6 ; -12) alors le vecteur –2. a pour coordonnées (-12 ; 24).
et –2. sont égaux, c'est donc qu'ils ont des coordonnées égales. Ainsi :
2nde solution. La plus calculatoire : on passe directement aux coordonnées. Point de vecteurs, nous allons travailler sur des nombres.
Comme 
(-2 – xC ; 5 – yC) et 
(4 – xC ; -7 – yC) alors le vecteur 
a pour coordonnées
( 3 × (-2 – xC) – 2 × (4 – xC) ; 3 × (5 – yC) – 2 × (-7 – yC)).
Ce qui réduit donne (- xC –14 ; -yC + 29).
Vu que les vecteurs et 
sont égaux, c'est donc qu'ils ont des coordonnées égales. Ainsi :
Quelques remarques sur cet exercice :
La géométrie analytique a été instituée pour simplifier la géométrie "classique" vectorielle. En effet, il est plus facile de travailler sur des nombres que sur des vecteurs. Cependant, dans certains cas, pour éviter de fastidieux calculs souvent générateurs d'erreurs(c'est le second cheminement), on peut avoir intérêt à simplifier le problème(comme cela a été fait avec la première solution).
Pour les paresseux qui ont à déterminer les coordonnées d'un point à partir d'une relation vectorielle, l'applette suivante peut être utile.
Applette déterminant les coordonnées d'un point défini par une égalité vectorielle.
Cette applette procède comme pour la seconde solution de l'exercice précédent. Autrement dit, c'est la méthode la plus fine !