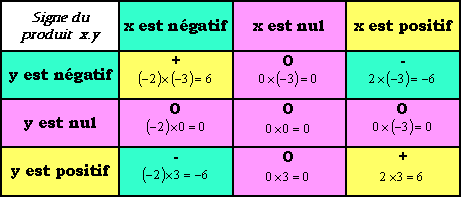
Quelques mots d'introduction :
Savoir que quelque chose est plus grand que 0 revient en fait à savoir qu'il est positif.
De même, quelque chose qui est plus petit que 0 est négatif !
C'est avec ces idées aussi évidentes que naturelles que l'on peut résoudre certaines inéquations..
Une expression ou un nombre peut être de trois signes.: positif, négatif ou nul.
Parfois, par positif, on entend positif ou nul.
Pour ce qui est de nos p'tites affaires, nous ferons la différence : quelque chose qui est nul (ou égal à 0) ne sera pas positif...ni négatif.

 

Signe d'un produit.
Si l'on connait le signe de deux facteurs, alors on connait celui de leur produit.
C'est ce que récapitule le tableau suivant :

 

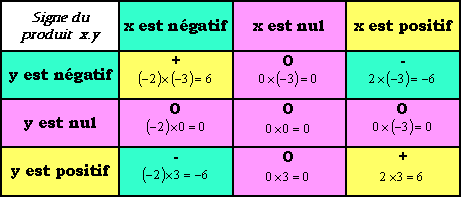
Signe d'un quotient.
Si l'on connait le signe du numérateur et celui du dénominateur, alors on connait le signe de la fraction.
C'est ce que récapitule le tableau suivant :

A peu de chose près, ce tableau ressemble à celui du produit. En effet, diviser revient en fait à multiplier par l'inverse !
Il existe quand même une différence avec le produit : on ne peut pas diviser par 0.
C'est peu de chose, et poutant c'est terriblement important !

 

Signe d'une somme ou d'une différence.
Même si l'on connait, le signe de deux nombres, il n'est guère aisé de connaitre le signe de leur somme ou de leur différence.
Par exemple, 3 est positif et -2 est négatif . Leur somme 3 + (-2) est positive et leur différence 3 - (-2) aussi.
Par contre, si l'on s'intéresse à 2 est positif et -3 est négatif . Leur somme 2 + (-3) est négative alors leur différence 2 - (-3) demeure positive.
En fait, il n'y a pas de règle générale. Mais dans certains cas particuliers, il est posssible de répondre.

Ce qui marche avec le produit et le quotient ne marche pas nécessairement avec la somme ou la différence. En ces circonstances, il faut donc faire preuve de prudence...

 

Quelques signes particuliers.
Certaines expressions ou certaines nombres ont des signes bien précis. Passons en revue ces cas particuliers :

Un carré est toujours positif ou nul.
Par exemple, si x est un réel quelconque (positif, négatif ou nul) alors x2 est toujours positif ou nul.
Par contre, x3 a même signe que le réel x.

La somme de deux nombres positifs est positive.
Par exemple, la somme x2 + 1 est toujours positive.
Par contre, la somme x2 - 1 est tanôt négative (pour x = 0), tantôt nulle (pour x = 1) ou encore positive (pour x = 2).
En effet, x2 - 1 est l'addition du réel positif ou nul x2 et du nombre négatif -1.

La somme de deux nombres négatifs est négative.
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Juin 1999/Janvier 2003. Tous droits réservés.