Cliquer ici pour cacher les solutions.

Utilisons la formule sin(-x) = -sin(x) au réel x = /6. Il vient alors que :

On applique la formule cos( – x) = -cos(x) au réel x = /6. Il vient alors que :

Une méthode consiste à déterminer la mesure principale d'un angle orienté de 61 /6. En effet deux mesures d'un même angle ont même sinus. Une autre consiste à écrire cette fraction sous la forme k × 2 + a où k est un entier naturel et a un réel. Nous opterons pour cette seconde solution. Remarquons que 2 = 12 /6. Par suite :

Ceci ayant été fait, il vient que :

On applique la formule cos²(x) + sin²(x) = 1. Ainsi :

Pour tout réel x tel que cos(x) ¹ 0,

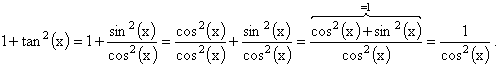
Remarquons que /6 = – 5 /6. On applique la formule sin( – x) = sin(x) au réel 5 /6 – x. Ainsi

Appelons M le point associé au réel a . Les coordonnées du point M sont donc (cos(a ) ; sin(a )). De plus M fait partie du cercle trigonométrique.

Dire que a est solution de l'équation cos(a ) = 0,5 équivaut à dire que l'abscisse du point M est égale à 0,5. Autrement dit que M fait partie de la droite d'équation x = 0,5.

Le point associé au réel a est donc le point d'intersection du cercle et de la droite d'équation x = 0,5. Représentons tout cela sur une figure.

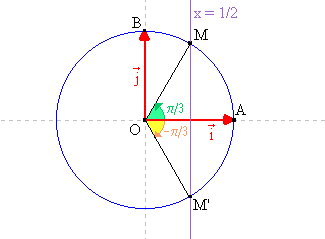
La droite d'équation x = 0,5 et le cercle trigonométrique ont deux points d'intersections : M et M'. Ils sont respectivement associés aux réels de la forme /3 + k × 2 et - /3 + k × 2 où k est un entier relatif.

En effet si M est associé à /3 alors il est aussi associé à tous les réels de la forme /3 + k × 2 . k représente un certain nombre de tours. Il en va de même pour M' et - /3.

Les solutions de cette équation sont les réels de cette forme. On résume tout cela par :

S = { /3 + k × 2 avec k entier relatif} È {- /3 + k × 2 avec k entier relatif}.

Autrement dit l'ensemble des solutions est formé de la réunion de l'ensemble des réels de la forme /3 + k × 2 et de celui des réels de la forme - /3 + k × 2 .

Cliquer ici pour cacher les solutions.