|
Dans ce qui suit ABC est un triangle.
On appelle A' le milieu du côté [BC], B' celui de [AC] et C' celui de [AB]. | 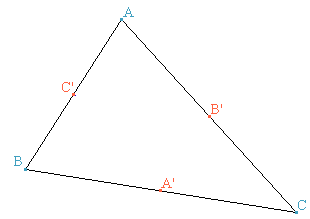 |
|
Dans ce qui suit ABC est un triangle.
On appelle A' le milieu du côté [BC], B' celui de [AC] et C' celui de [AB]. |  |
Au travers de cette petite aventure, nous allons démontrer rigoureusement que le seul point G vérifiant ![]() est le point de concours des trois médianes du triangle (ABC). Cela s'effectuera en deux étapes, en deux propositions. Au terme, nous pourrons conclure par le théorème.
est le point de concours des trois médianes du triangle (ABC). Cela s'effectuera en deux étapes, en deux propositions. Au terme, nous pourrons conclure par le théorème.

Quelques commentaires sur ce théorème.
 A priori, nul ne peut dire combien il existe de point G vérifiant l'égalité
A priori, nul ne peut dire combien il existe de point G vérifiant l'égalité ![]() . C'est pour cela que nous devons prouver qu'il n'en existe qu'un seul. C'est le point (i) de la proposition 1.
. C'est pour cela que nous devons prouver qu'il n'en existe qu'un seul. C'est le point (i) de la proposition 1.
 On vous a toujours dit que les trois médianes d'un triangle étaient concourantes en un point que l'on appelait centre de gravité. Seulement, on ne vous l'a sûrement jamais démontré. Nous comblerons cet oubli en prouvant ce point (ii).
On vous a toujours dit que les trois médianes d'un triangle étaient concourantes en un point que l'on appelait centre de gravité. Seulement, on ne vous l'a sûrement jamais démontré. Nous comblerons cet oubli en prouvant ce point (ii).
La preuve de cette proposition 1 :
Nous allons démontrer successivement chacun des deux points.
(i) : Soit G un point du plan tel que ![]() . On peut alors écrire que :
. On peut alors écrire que :
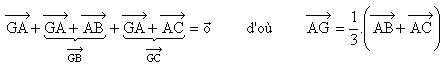
(ii) : Pour démontrer que les trois médianes sont concourantes, nous allons prouver que G appartient à chacune des trois médianes.
Au point (i), nous avons démontré que G vérifie l'égalité :
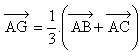
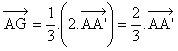
Ce que nous venons de montrer avec la médiane (AA') est aussi vrai pour les deux autres médianes. En effet :
Pour la médiane (BB'), en partant de ![]() , on peut écrire que :
, on peut écrire que :
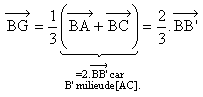
Pour la médiane (CC'), on peut écrire que :
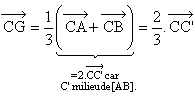
En résumé, le point G fait donc partie des trois médianes (AA'), (BB') et (CC').
Ces trois droites sont donc concourantes et le point G en est le point d'intersection.
Nous venons de démontrer qu'il existe un et un seul point G tel que ![]() et qu'il est nécessairement le centre de gravité du triangle (ABC).
et qu'il est nécessairement le centre de gravité du triangle (ABC).
Mais réciproquement, si un point S est le centre de gravité du triangle (ABC), peut-on affirmer qu'il vérifie l'égalité vectorielle ![]() .
.
C'est l'objet de la proposition 2.

La preuve de cette proposition :
On appelle D le symétrique de A par rapport à G.
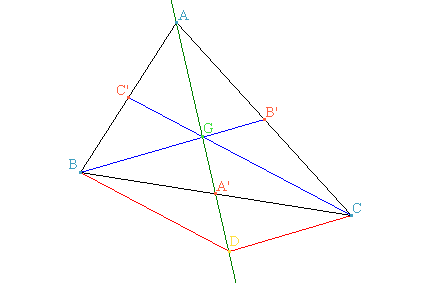
Le point G est donc le milieu du segment [AD]. Donc : ![]() .
.
Intéressons-nous au quadrilatère (GCDB).
Dans le triangle (ABD), C' est le milieu du coté [AB] et G celui de [AD].
En application du théorème des milieux, la droite (GC') est donc parallèle au côté (BD).
Autrement appelé, la droite (GC) est donc parallèle à (BD).
Dans le triangle (ACD), B' est le milieu du côté [AC] et G celui du côté [AD].
Toujours en application du théorème des milieux, la droite (GB') est donc parallèle au côté (CD).
Autrement écrit, la droite (BG) est parallèle à (CD).
En résumé, (GCDB) est un quadrilatère dont les côtés opposés sont parallèles deux à deux.
C'est donc un parallélogramme.
La règle du parallélogramme est donc applicable dans (GCDB). On peut donc écrire que :
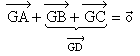
Autrement dit, ce que l'on voulait !
Ces deux propositions ayant été démontrées, la boucle est bouclée. Nous pouvons à présent affirmer que :

Note :
La démonstration du point (ii) de la proposition 1 nous permet de dire que :
Le centre de gravité d'un triangle se trouve aux deux tiers de la médiane à partir du sommet.
C'était là-dessus que s'appuyait notre mensonge...