| Décomposer une fonction rationnelle avec la division euclidienne |
On considère la fonction rationelle f définie pour tout réel x ¹ -3 par :
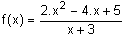
On sait que f peut être écrite sous la forme :
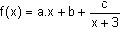
On appelle P le numérateur de la fonction rationnelle f.
Q est son dénominateur.
Ainsi, pour tout x :
|
P(x) = 2.x2 - 4.x + 5
Q(x) = x + 3 |
La division euclidienne du polynôme P par le polynôme Q donne pour résultat :
Autrement dit, pour tout x :
Introduisons ce résultat dans l'expression de f(x).
Pour tout réel x :
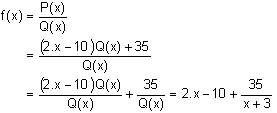
Conclusion : pour tout réel x ¹ -3 :
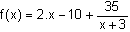
Comme vous avez pu le constater, la division euclidienne est une méthode de décomposition rapide et efficace. A condition bien sûr de savoir la faire...
Précisons tout de même que cette méthode est à réserver aux fonctions rationnelles dont le dénominateur est simple. Si elle marche parfaitement avec f et g, elle est en revanche inopérante sur la fonction h.
Rappelons que pour tout x :
