Avant de nous intéresser à l'étude des fonctions trinomiales en général, nous allons nous intéresser à quelques cas particuliers.
Premier de ces cas particuliers, la fonction f définie par :

Ensemble de définition de cette fonction f.
Celui-ci n'étant pas fourni, nous devons le déterminer. La question que nous devons nous poser est :

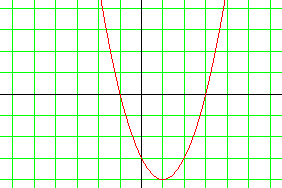
Courbe représentative.
La courbe représentative de la fonction f est la courbe d'équation   y = x² - 2.x - 3. C'est une parabole.

• Sur l'intervalle ]-¥ ; 1] :
  Lorsque x et y sont plus petits que 1, alors y + x < 2
  donc le facteur y + x - 2 est négatif.
  donc la différence f(y) - f(x) est négative.
  En résumé sur l'intervalle ]-¥ ; 1] :
  Si   x < y   alors   f(y) - f(x) < 0   ;Û   f(x) > f(y).
  Donc la fonction f est décroissante sur cet intervalle.
   
• Sur l'intervalle [1 ; +¥[ :
  Lorsque x et y sont plus grands que 1, alors y + x > 2
  donc le facteur y + x - 2 est positif.
  donc la différence f(y) - f(x) est positive.
  En résumé sur l'intervalle [1 ; +¥[ :
  Si   x < y   alors   f(y) - f(x) > 0   Û   f(x) < f(y).
  Donc la fonction f est croissante sur [1 ; +¥[.

Antécédents de 0 par cette fonction f.
Déterminer les antécédents de 0 par la fonction f permet d'aborder le délicat problème de la résolution d'équations du second degré (celles en x²).
Lorsque nous étudierons le cas général, nous mettrons sur pied un mécanisme permettant la résolution d'équations de la forme   a.x² + b.x + c = 0.
En attendant ce magnifique instant, voyons comment il est possible de faire autrement !

Pour trouver les antécédents de 0, nous devons résoudre l'équation   f(x) = 0.
Ce genre d'équation du second degré se résout sans problème mais avec quelques astuces. Le fondement de notre manoeuvre est la factorisation d'une expression de second degré.
D'après sa courbe, la fonction f doit donner à 0 deux antécédents. Voyons par le calcul ce qu'il en est.

Signe du trinôme x² - 2.x - 3.
L'objectif de ce paragraphe est de connaître le signe de f(x) en fonction de x.
Pour parvenir à nos fins, il nous faut déterminer le ou les antécédents de 0 par f.
D'après ce qui vient d'être fait, nous pouvons dire que les deux antécédents de 0 par f sont -1 et 3.
Positionnons -1 et 3 dans le tableau de variation de cette fonction f.

• f(x) est positif lorsque x est plus petit que -1 ou lorsque x est plus grand que 3.
• f(x) est nul lorsque x est égal à -1 ou à 3.
• f(x) est négatif lorsque x est compris strictement entre -1 et 3.

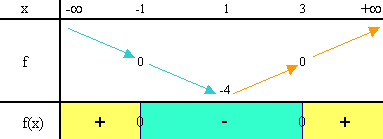
Un autre chemin...
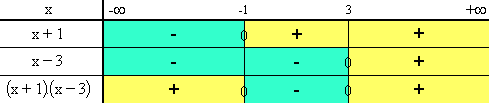
Nous aurions pu aussi dresser le tableau de signe de f(x) en utilisant le signe d'un produit.
En effet, on montre que pour tout réel x,