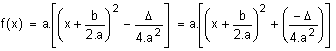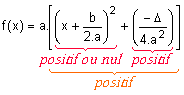Après avoir étudier trois fonctions du second degré particulières, nous allons étudier ces fonctions en général.
Nous suivrons globalement le même plan que pour les trois exemples...
Etudions la fonction f définie par :
f(x) = a.x2 + b.x + c
On dit que f est un trinôme car c'est une somme de trois termes ou "nômes".
On qualifie aussi f de fonction du second degré. En effet :
f(x) = a.x + b.x + c
Dans l'expression de f(x), la puissance de x la plus élevée est une puissance 2. D'où la qualification de "second degré".
Mais quid des fonctions du premier degré ?
En fait une fonction du premier degré est une fonction g de la forme :
g(x) = a.x + b
Autrement dit, c'est une fonction affine.
Ensemble de définition de cette fonction f.
f(x) est une somme de carrés et de produits. Tous les réels x ont une image par cette fonction f.
Donc :
Df = R
L'étude de la fonction f se fera donc sur l'intervalle ]-¥ ; +¥[.
Courbe représentative.
La courbe représentative de toute fonction du second degré est une parabole.
Celle-ci a pour équation y = a.x2 + b.x + c.
En simplifiant, on peut dire qu'il y a deux grandes familles de courbes. La différence se fait suivant le signe de a.
|
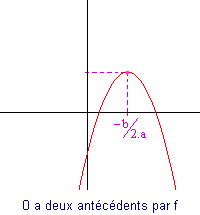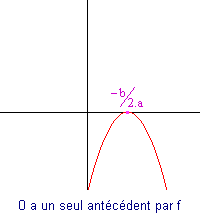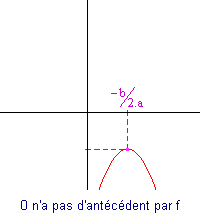
Si a est négatif alors la courbe de f est la suivante :
|
Si a est positif alors la courbe de f est la suivante :
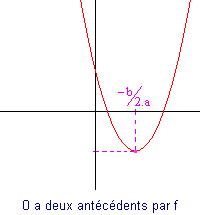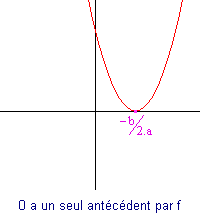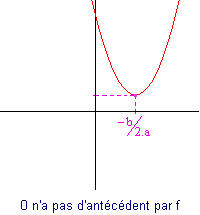
|
Dans les deux cas :
- Le sommet de la parabole est atteint pour x = -b/(2.a).
- La courbe ne franchit pas nécessairement l'axe des abscisses. Elle peut le tutoyer ou l'ignorer...
Variations de la fonction f.
Comme l'ont montré les trois exemples que nous avons vu, du point de vue des variations il y a deux catégories de fonctions du second degré :
- Celles dont le coefficient dominant a est négatif.
- Celles dont le coefficient dominant a est positif.
Globalement, les raisonnements conduisant aux résultats suivants sont les mêmes que ceux vus avec nos trois exemples.
Ainsi :
|
Si a est négatif alors
le tableau de variation de la fonction f est donc :
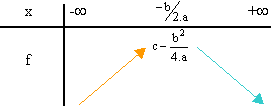
Conséquence : f admet un maximum
en x = -b/(2.a). Il vaut c - b2/(4.a).
Un exemple d'une telle fonction est :
- g(x) = -2.x2 + 6.x - 4,5.
|
Si a est positif alors le tableau de variation de la fonction f est donc :
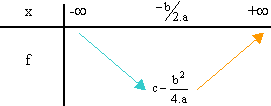
Conséquence : f admet un minimum
en x = -b/(2.a). Il vaut c - b2/(4.a).
Deux exemples d'une telle fonction sont :
- f(x) = x2 - 2.x - 3
- h(x) = x2 - 4.x + 7
|
Pour savoir pourquoi il en est ainsi, cliquer sur le tableau de variation correspondant...
Antécédents de 0 par cette fonction f.
Pour déterminer les antécédents de 0, nous devons résoudre l'équation f(x) = 0.
Autrement dit, nous devons résoudre l'équation du second degré :
a.x2 + b.x + c = 0
où a, b et c sont des nombres et où l'inconnue est x.
Comme nous l'avons déjà observé avec sa courbe, par une fonction du second degré, 0 peut avoir un, deux ou aucun antécédent.
Autrement dit, une équation du second degré peut voir une, deux ou aucune solution.
Pour connaître le nombre de solutions d'une équation du second degré, on introduit un indicateur : le discriminant  .
.

Pour connaître le pourquoi de la chose, cliquer sur ce théorème...
Conclusion : Les antécédents de 0 sont les solutions de l'équation...
Signe du trinôme a.x2 + b.x + c.
Déterminons le signe du trinôme f(x) en fonction de x.
Nous l'avons vu avec nos trois exemples, pour déterminer le signe d'une expression
il faut :
- soit factoriser l'expression et l'écrire sous la forme d'un produit de facteurs dont l'on connaît le signe.
- soit modifier l'expression en quelques chose de plus exploitable.
Le discriminant de l'expression a.x2 + b.x + c est le réel  tel que :
tel que :
 = b2 - 4.a.c
On montre
que pour tout réel x :
= b2 - 4.a.c
On montre
que pour tout réel x :
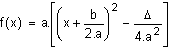
A partir de là, tout dépend du signe du discriminant  :
:
- Si
 est positif alors
est positif alors
l'équation a.x2 + b.x + c = 0 admet deux solutions x1 et x1.
Le trinôme f(x) se factorise sans problème. Ainsi :
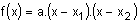 f(x) est donc le produit des facteurs a, x - x1 et x - x2.
f(x) est donc le produit des facteurs a, x - x1 et x - x2.
Le tableau de signe de l'expression f(x) ne pose alors aucun problème !
Un exemple d'une telle fonction est la fonction f(x) = x2 - 2.x - 3.
- Si
 est nul alors
est nul alors
l'équation a.x2 + b.x + c = 0 admet une seule solution x1 = -b/(2.a).
Le trinôme f(x) se factorise (quasiment automatiquement). Ainsi :
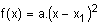 f(x) est donc le produit du réel a et d'un carré. En clair :
f(x) est donc le produit du réel a et d'un carré. En clair :
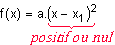 Le signe de l'expression f(x) est donc quasiment toujours le signe de a...
Le signe de l'expression f(x) est donc quasiment toujours le signe de a...
sauf en -b/2.a !
D'où le tableau de signe suivant :

Un exemple d'une telle fonction est la fonction g(x) = -2.x2 + 6.x - 4,5.
- Si
 est négatif alors
est négatif alors
l'équation a.x2 + b.x + c = 0 n'admet aucune solution.
On peut écrire que :
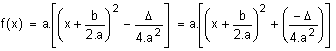 Intéressons nous au signe de ce produit :
Intéressons nous au signe de ce produit :

Ainsi :
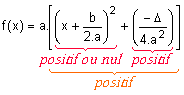 f(x) est donc le produit du réel a et d'un autre facteur qui est toujours positif.
f(x) est donc le produit du réel a et d'un autre facteur qui est toujours positif.
Le signe de l'expression f(x) est donc toujours le signe de a...
D'où le tableau de signe suivant :

Un exemple d'une telle fonction est la fonction h(x) = x2 - 4.x + 7.
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par
la taverne de l'Irlandais.
(c) AMLTI Juillet 1999/Janvier 2003. Tous droits réservés.

 .
.

 tel que :
tel que :
 = b2 - 4.a.c
= b2 - 4.a.c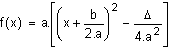
 :
:
 est positif alors
est positif alors
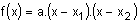
 est nul alors
est nul alors
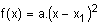
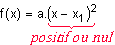

 est négatif alors
est négatif alors