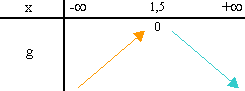Etude de  g(x) = -2.x² + 6.x - 4,5

Avant de nous intéresser à l'étude des fonctions trinomiales en général, nous allons nous intéresser à quelques cas particuliers.
Etudions la fonction g définie par :

g(x) = -2.x2 + 6.x - 4,5
Cette seconde fonction g est tout autant "trinomiale" que la première.
Ici,   a = -2     b = 6 et   c = -4,5.

 

Ensemble de définition de cette fonction f.
g(x) est une somme de carrés et de produits. Tous les réels x ont une image par cette fonction f.
Donc :

Dg = R
L'étude de la fonction se fera donc sur l'intervalle ]-¥ ; +¥[.

 

Courbe représentative.
La courbe représentative de la fonction g est la courbe d'équation   y = -2.x2 + 6.x - 4,5. C'est aussi une parabole.


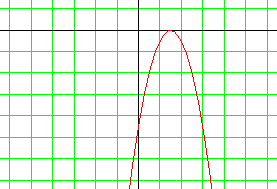
Graphiquement, on constate que la courbe est croissante sur l'intervalle ]-¥ ; 1,5] et décroissante sur l'intervalle [1,5 ; +¥[.
Il semble également que 0 ait un seul antécédent par g.
Nous démontrerons dans les deux prochains paragraphes ces constatations.

 

Variations de la fonction g.
Soient x et y deux réels tels que   x < y.
Notre but est toujours de connaître le signe de la différence   g(y) - g(x) dans certains cas précis.
Essayons d'exprimer cette différence sous la forme d'un produit.

g(y) - g(x)2 = (-2.y2 + 6.y - 4,5) - (-2.x2 + 6.x - 4,5)
= -2.y2 + 6.y - 4,5 + 2.x2 - 6.x + 4,5
= - 2.y2 + 2.x2 + 6.y - 6.x
= -2 (y2 - x2) + 6.(y - x)
= -2 (y - x).(y + x) + 6.(y - x)
= (y - x) . [-2.(y + x) + 6]
Cette différence peut donc s'exprimer sous la forme d'un produit. A présent, nous pouvons commencer la manoeuvre.
Comme y est plus grand que x alors le facteur   y - x   est positif.
De plus :
Le tableau de variation de la fonction g est donc :
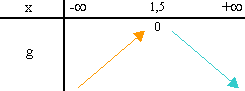
Encore une fois, c'est pas trop compliqué !

Conséquence : A la lecture de son tableau de variation, on peut dire g admet un maximum en x = 1,5. Il vaut 0.

 

Antécédents de 0 par cette fonction g.
Comme cela a déjà été dit, chercher les antécédents de 0 permet de résoudre autrement des équations du second degré.
Pour trouver les antécédents de 0, nous devons résoudre l'équation   g(x) = 0.
Les visionnaires feront tout pour ramener à une identité remarquable de la forme (x - a)2.
Les autres procéderont comme pour la fonction f.
Nous ferons comme "les autres".
D'après sa courbe, la fonction f doit donner à 0 deux antécédents. Au boulot !

g(x) = 02 équivaut à   -2.x2 + 6.x - 4,5 = 0
équivaut à   -2.(x2 - 3.x + 2,25) = 0
équivaut à   x2 - 3.x + 2,25 = 0/(-2)
équivaut à   x2 - 3.x + 2,25 = 0
équivaut à   x2 - 2.(1,5).x + 2,25 = 0
équivaut à   (x - 1,5)2 - (1,5)2 + 2,25 = 0
équivaut à   (x - 1,5)2 - 2,25 + 2,25 = 0
équivaut à   (x - 1,5)2 = 0
équivaut à   (x - 1,5) = 0
équivaut à   x = 1,5
Donc l'unique antécédent de 0 par la fonction g est 1,5.

 

Signe du trinôme -2.x2 + 6.x - 4,5.
Déterminons le signe du trinôme g(x) en fonction de x.
En fait, à partir du tableau de variation de g, il est déjà possible de répondre à la question.

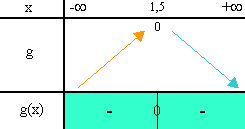Jamais un signe n'aura été fait aussi vite !
Donc, en résumé :

Un autre chemin...
Nous aurions pu aussi dresser le tableau de signe de g(x) en utilisant le fait que certaines expressions ont un signe très particulier.
En effet, on montre que pour tout réel x,

g(x) = -2 . (x - 1,5)2
Il suffit de voir la manière dont ont été déterminés les antécédents de 0
g(x) est donc le produit du réel négatif -2 et du carré (x - 1,5)2.
Or un carré est toujours positif ou nul !
Donc le produit g(x) sera toujours négatif ou nul.
Vu que l'on connaît les antécédents de 0 par g, le tableau de signe de g(x) est donc :
g(x) ne peut être que négatif ou nul... Quand il n'est pas l'un, il est l'autre !

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Juillet 1999/Janvier 2003. Tous droits réservés.