
Les opérations sur les limites ne permettent pas toujours de déterminer la limite d'une fonction. Il faut alors changer de chemin et modifier l'écriture de cette fonction... afin de pouvoir les appliquer !
Nous allons voir comment il est possible de connaître à coup sûr la limite à l'infini d'un polynôme ou d'une fonction rationnelle. Ou encore d'autres fonctions...
Limites de polynômes et fonctions rationnelles
Limite d'un polynôme.
Déterminons la limite en +¥ du polynôme f défini pour tout réel x par :
Au premier abord, lorsque x tend vers +¥ :

L'actuelle écriture de f ne permet pas de conclure. Modifions la.

L'écriture modifiée, nous allons pouvoir manoeuvrer.
Lorsque x tend vers +¥ :
 Donc :
Donc :

De plus, lorsque x tend vers +¥, nous savons que 3.x3 s'en va vers +¥.
Connaissant les limites des deux facteurs, nous pouvons connaître celle de leur produit f(x).

Une remarque :
Si on observe attentivement ce qui vient de se passer, on remarque que c'est 3.x3 qui a imposé sa limite au produit.
Or 3.x3 est le terme dominant du polynôme f(x).
Ce qui est vrai pour le cas particulier f l'est pour n'importe quel polynôme. C'est-à-dire :

Par exemple :


Limite d'une fraction rationnelle.
On considère la fonction rationnelle g définie pour tout réel x par :

Au premier abord, en utilisant ce que nous avons fait avec les polynômes, nous pouvons dire que lorsque x tend vers +¥ :

La présente écriture de g ne permet pas de conclure. Il nous faut donc la modifier.

Cette dernière écriture de la fonction rationnelle g est plus exploitable. Illustration :


Connaissant les limites des deux facteurs, celle de leur produit g(x) est à notre portée.

Une remarque (encore !) :
Si on observe attentivement ce qui vient de se passer, on remarque que c'est  qui a imposé sa limite au produit.
qui a imposé sa limite au produit.
Or si l'on y regarde de plus près, on constate que :


Par exemple :
 en -¥ et +¥ sont celles du quotient de ses deux termes dominants
en -¥ et +¥ sont celles du quotient de ses deux termes dominants  .
.
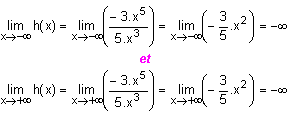
 en -¥ et +¥ sont celles du quotient de ses deux termes dominants
en -¥ et +¥ sont celles du quotient de ses deux termes dominants  .
.

Une fonction avec une racine.
Nous avons vu comment déterminer les limites aux infinis d'un polynôme. Compliquons le problème en y rajoutant une racine carrée...
Déterminons la limite en +¥ de la fonction f définie pour tout x par :
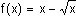
A première vue :
Lorsque x tend vers +¥, les fonctions x et  s'envolent toutes deux vers +¥.
s'envolent toutes deux vers +¥.
Ainsi :

Transformons la somme en produit. Pour cela, nous allons factoriser par x.


La limite de f lorsque x tend vers +¥ est donc égale à +¥.
Une remarque :
On remarque que c'est en fait x qui impose sa limite.
Car la règle que nous avons vu pour les polynômes est aussi applicable à ce genre de fonction. En effet :

 .
.
Une fonction avec deux racines.
Dans les trois précédents paragraphe, le truc qui permettait de s'en sortir consistait à factoriser par le terme de plus haut degré. Mais cet artifice a ses limites. La preuve avec ce qui suit :
Déterminons la limite en +¥ de la fonction g définie pour tout x par :

De prime abord :
Lorsque x va vers +¥, les fonctions  et
et  s'en vont comme deux soeurs vers +¥.
s'en vont comme deux soeurs vers +¥.
Autrement dit :

Nous pourrions factoriser mais cela ne conduirait à rien. Pour connaître la limite de g en +¥, nous allons multiplier  par sa quantité conjuguée.
par sa quantité conjuguée.

A partir de là, nous pouvons conclure :
Lorsque x va vers +¥,  s'en va vers +¥. Donc g(x) tend vers 0.
s'en va vers +¥. Donc g(x) tend vers 0.
Ainsi :
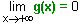
Un mot de conclusion :
Comme nous l'avons vu au travers des quatre paragraphes précédents, il existe diverses manières permettant de lever une indétermination quant à une limite.
Même s'il n'existe pas de "recette miracle", évoquons quelques pistes :