
Parfois, il n'est pas possible de connaître la limite d'une fonction quelque part. Cependant, il arrive qu'une autre fonction permette de solutionner le problème. C'est l'objet et l'intérêt des théorèmes de comparaisons...
Nous n'évoquerons que le cas des limites aux infinis. Pour ce qui est des limites en un point, c'est à peu près pareil mais en plus ponctuel !
Comparaisons à l'infini.
Le théorème suivant est très visuel. En comparant deux fonctions, connaissant la limite de l'une, il est parfois possible de déterminer la limite de l'autre. Illustration avec le théorème que voilà !

Examinons quelques exemples :
De façon à se avoir une idée de la situation, traçons la courbe représentative de cette fonction f.
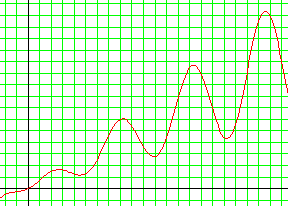
Il semble que la fonction f hésite quant à l'attitude à adopter : elle monte, elle descend. Mais où va-t-elle donc ?
La réponse va venir du précédent théorème.
On peut écrire que pour tout réel positif :
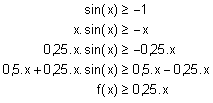
 |
Lorsque x tend +¥, la fonction 0,25 . x tend vers +¥.
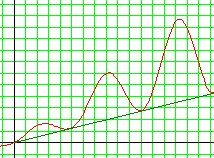
Vu qu'en allant vers +¥, f(x) est toujours plus grand que 0,25 . x alors la limite de f est aussi égale à +¥. Ainsi : 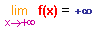 |
L'indécision initiale était en fait prévisible rien qu'en observant la croissance moyenne de la courbe de f...
Nous n'avons vu les théorèmes de comparaison qu'aux infinis. Nous aurions pu aussi préciser qu'ils pouvaient s'appliquer en un point.
C'est par exemple, le cas de la fonction suivante...
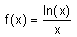
L'ensemble de définition de cette fonction f est ]0 ; +¥[.
Autrement dit, l'approche de 0 ne pourra se faire que par la droite...
Pour avoir une idée de cette limite en 0, traçons la courbe de cette fonction f :
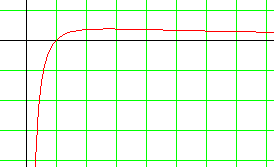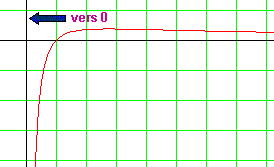
Lorsque x se rapproche de 0, f(x) semble plonger vers -¥.
Démontrons cette constatation en utilisant une comparaison.
Lorsque x est compris entre 0 et 1, on sait que :


A l'approche de 0, la fonction f est donc majorée par la fonction logarithme.
Or lorsque x tend vers 0, cette dernière a pour limite -¥.
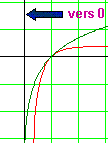 |
Majorée par une fonction qui s'approchant de 0 plonge vers les abysses, f ne peut échapper au même sort...
Autrement écrit : 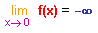 |
Nous aurions être plus économique dans notre manière de procéder.
En effet, ln(x)/x est à l'approche de 0 le quotient d'une chose qui va vers -¥ et d'une autre qui va vers 0 par valeurs positives...
Comme l'ont montré les deux précédents exemples, l'essentiel du travail consiste à obtenir l'inégalité qui permet la comparaison...
Théorème des gendarmes.
Coincé entre deux policiers, un suspect a peu de chances de s'échapper. Il ira là où ses gardiens se rendront.
Ce qui est vrai pour les poulets et les voleurs, l'est aussi pour les fonctions. C'est le théorème des "gendarmes".

Examinons quelques exemples :
A titre informatif, traçons la courbe représentative de la fonction f.
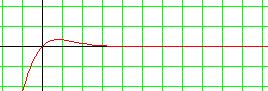
Il semble qu'à l'infini, la limite de la fonction f soit égale à 0.
Le reste de notre travail va consister à montrer cette constatation.
Lorsque x s'en va vers +¥ :
Pour tout réel x, on sait que :
 sin(x)
sin(x)  1
1 f(x)
f(x)  e-x
e-xOr lorsque x tend vers +¥, -e-x et e-x tendent vers 0.
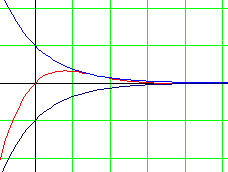 |
Coincé entre deux machins qui tendent vers 0, en vertu du théorème des gendarmes et en toute logique f(x) ne peut aller que vers 0.
Ainsi : 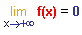 |
 , lorsque x va vers 0.
, lorsque x va vers 0.
