Une dérivée non continue.

Intéressons à la fonction f définie par : f(0) = 0. Pour tout réel x non nul,   f(x) = x2 . Nous allons montrer que cette fonction est continue sur ]-¥ ; +¥[, puis y est dérivable mais que sa dérivée n'est pas continue en 0.

La fonction f est-elle continue sur ]-¥ ; +¥[ ?
Partout sauf en 0, la fonction f est le produit de la fonction carrée et de .
Ces deux fonctions étant continues sur ]-¥ ; 0[ et sur ]0 ; +¥[, il en va de même pour leur produit : donc f est continue sur  ]-¥ ; 1[ È ]1 ; +¥[.

Reste le cas de 0.

Pour démontrer que f est continue en 0, nous devons prouver que lorsque x tend vers 0, f(x) tend vers f(0). Autrement écrit, nous devons établir que :

Pour y arriver, nous allons essayer d'encadrer ou de "coincer" la différence |f(x) - f(0)|. Nous allons faire en sorte de la majorer par quelque chose de plus parlant..

Pour tout x non nul, on peut écrire que :

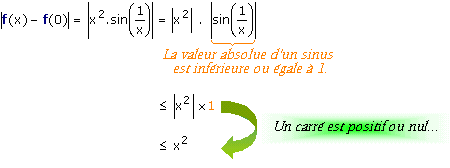
Or lorsque x tend vers 0, x² tend aussi vers 0. Autrement écrit :

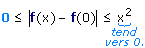
En application du théorème des gendarmes, nous pouvons dire que lorsque x tend vers vers 0, |f(x) - f(0)| tend aussi vers 0.
Donc la limite de f(x) en 0 est bien f(0).
Donc f est aussi continue en 0.

La fonction f est-elle dérivable sur ]-¥ ; +¥[ ?
Nous allons faire pour la dérivabilité de la fonction f ce que nous avons fait pour la continuité : nous allons envisager deux cas :

• Lorsque x est différent de 0 :
  Sur les intervalles ]-¥ ; 0[ et ]0 ; +¥[, la fonction f est dérivable car elle est le produit de deux fonctions qui y sont dérivables : x² et .
  Nous pouvons donc calculer cette dérivée f'. Nous utiliserons la formule de dérivation du produit.
  Pour tout réel x non nul :
   
• Lorsque x est égal à 0 :
  Pour voir si la fonction f est dérivable en 0, nous allons nous intéresser à la limite lorsque h tend vers 0 du quotient .
  Pour tout réel non nul h, on peut écrire que :
  Or lorsque h tend vers 0 :
  
  Coincé entre 0 et une fonction qui y tend, le quotient a donc lui aussi pour limite 0.
  Donc la fonction f est dérivable en 0. De plus :  f'(0) = 0.

La dérivée f' est-elle continue sur ]-¥ ; +¥[ ?
Jusqu'à présent toutes les dérivées que nous connaissons sont continues. Cet état de fait va prendre fin avec ce qui suit :

Il est clair que la fonction  f'(x) =   est continue sur les intervalles ]-¥ ; 0[ et ]0 ; +¥[.
Par contre en 0, la continuité n'est pas acquise ! Nous devons approfondir la question.

Là encore, pour démontrer que la fonction f' est continue en 0, nous allons devoir prouver que lorsque x tend vers 0, tend vers f'(0), c'est-à-dire vers 0. A voir la courbe de f', la chose ne semble guère aisée.

En fait :

Autrement dit, lorsque x tend vers 0, f'(x) n'a pas de limite à cause de .

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) Juin 2000/Janvier 2003. Tous droits réservés.