L'exponentielle est au programme de toutes les séries de Terminale pour lesquelles le mot "mathématiques" est porteur de sens. Pour ce qui nous concerne, nous nous efforcerons de lui en donner un.

L'exponentielle est la seconde des deux fonctions introduites en Terminale.
On la définit comme étant la réciproque du logarithme népérien. Toutes les propriétés d'exp (c'est son p'tit nom) viennent d'ailleurs de ln.
Voici donc l'histoire de celle qui est la moitié de ln : l'exponentielle.

Au commencement.
Au commencement, était la fonction logarithme népérien.
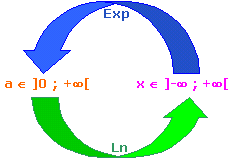
Comme elle était une bijection de ]0 ; +[ sur ]- ; +[, elle admettait donc une réciproque. Ainsi naquit l'exponentielle...
 

Quelques remarques sur cette copieuse définition :

• Nous connaissons d'emblée  exp(0).
  En effet, comme  ln(1) = 0  alors  nous pouvons écrire que  1 = exp(0).
   
• A la manière d'un couple de rivaux, ln et exp s'annihilent. En effet :
  

  Si a est un réel strictement positif  alors   exp[ln(a)] = a. Si x est un réel quelconque  alors   ln[exp(x)] = x. L'une est la réciproque de l'autre.

   
• Le nombre e est l'image de 1 par la fonction exponentielle. Autrement écrit :   e = exp(1) = e¹.
  Une valeur approchée de ce nombre e est 2,71828182845904...
   
• Si l'on connaît la courbe de la fonction logarithme népérien  alors  on peut tracer celle de exp.
    

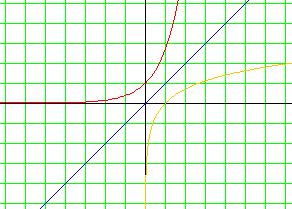  La courbe de la fonction exponentielle est la symétrique de celle de la fonction logarithme népérien par rapport à la droite d'équation  y = x. Car pour passer de ln à exp, il suffit simplement d'intervertir abscisse et ordonnée... Pou note, la droite d'équation y = x  est aussi appelée première bissectrice du plan.

A partir de cette définition, nous allons pouvoir étudier rapidement la fonction exponentielle.

La fonction exponentielle.
Exp est définie sur ]- ; +[. Nous allons étudier celle-ci sur cet intervalle.
Tout ce qui va suivre va aller très vite car ce ne sont en fait que les conséquences de choses que nous avons déjà vues...

1. Première étape : est-elle dérivable sur son ensemble de définition  ?
   Comme la fonction ln est dérivable sur l'intervalle ]0 ; +[ et que exp ne s'annule pas sur ]- ; +[   alors   la fonction exponentielle est dérivable sur ]- ; +[.
   De plus, pour tout réel x :

   

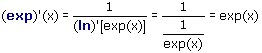
   Conclusion : la fonction exponentielle est dérivable sur ]- ; +[. De plus, elle est sa propre dérivée.

    
2. Seconde étape : les variations de la fonction exponentielle ?
   Comme pour tout réel x, exp(x) est strictement positif   alors   la fonction exponentielle est strictement croissante.
   Précisons à ceux qui l'auraient déjà oublié que exp est sa propre dérivée.
        

   Conclusion : la fonction exponentielle est strictement croissante sur ]- ; +[.

    
3. Troisième étape : les limites de la fonction exponentielle ?
   La fonction exponentielle a au mieux deux limites : un en - et une autre de l'autre côté en +. 
   Pour les obtenir, nous allons nous servir de celles de ln.

   Si l'on connaît le logarithme népérien  alors  on connaît l'exponentielle. En effet :

   exp(x) = y   équivaut à   x = ln(y)C'est la stricte application de la définition !

   Lorsque y tend vers 0,  x = ln(y)  tend vers -.
   Donc, réciproquement, lorsque x tend vers -, alors  y = exp(x)  tend vers 0.

   De même :
   Lorsque y tend vers +,  x = ln(y)  tend vers +.
   Réciproquement, lorsque x tend vers +, alors  y = exp(x)  tend vers +.

   Conclusion : la fonction exponentielle admet deux limites en - et en +.           L'axe des abscisses est une asymptote à la courbe de exp au voisinage de -.

    

Nous pouvons à présent dresser le tableau de variation de la fonction exponentielle.

Les propriétés de l'exponentielle.
A l'instar de ln, la fonction exponentielle a des propriétés d'alchimistes. Cette première transforme les produits et les quotients en sommes et différences. Exp fait la même chose... mais à l'envers !
Voyons ces propriétés dans le détail.

Généralement, lorsque l'on a une certaine propriété sur le produit, il est bien rare qu'il n'y ait pas de conséquences sur l' inverse, le quotient, la puissance ou la racine carrée.
L'exponentielle fait partie de cette généralité...

Autres propriétés : Si a et b sont deux réels, et n un entier relatif  alors :   ii. = e-a iii. = ea-b iv. (ea)n = en.a  v. = e½.a

Ces quatre propriétés permettent de simplifier certaines expressions. Par exemple : = e½.(2.x+1) = ex+½ (e3.x+1)2 = e2 × (3.x+1) = e6.x+2 Comme la première, ces quatre propriétés servent principalement à déterminer des limites. Dans certains cas, elles permettent de dériver à moindre frais.

Les preuves de ces propriétés : en s'inspirant de ce qui a été fait pour la première propriété, il est assez aisé de démontrer celles-ci. Par paresse et par un manque évident de volonté, nous laisserons ces diverses démonstrations à la discrétion de notre vénéré(e) lecteur(rice) !

Des trucs en plus.
Pour achever notre aventure exponentielle, nous allons aborder cinq situations où exp intervient. Nous allons voir comment ils peuvent être résolus, moyennant un peu de bon sens.
Au sommaire :

A présent, nous pouvons entamer les hostilités ! 

Après les équations, nous allons voir comment il est possible de dériver à moindre frais : sans trop d'effort !

Dériver à moindre frais un quotient d'exponentielles

Dérivons la fonction f(x) = qui est définie et dérivable sur l'intervalle ]- ; +[. Pour effectuer ce travail, il y a deux méthodes : la directe qui est la plus calculatoire ou bien l'intelligente qui consiste à simplifier au préalable l'écriture de f(x), puis à la dérivée. Voyons ces deux manières en action. Précisons avant cela une chose : si u est une fonction dérivable   alors  la dérivée de la composée  eu  est   u' . eu. C'est là, la stricte application de la formule de dérivation d'une fonction composée. La méthode directe   La méthode "intelligente" Nous allons dériver le quotient avec la formule prévue à cet effet. Pour tout réel x, on peut écrire que : On imagine la suite de ces très barbares calculs ! Si on ne se trompe pas (ce qui est assez dur!), on arrive à la fin à :  f'(x) = ex+2 Précédemment, nous avons vu une formule permettant de simplifier un quotient d'exponentielles : c'était la propriété iii. Modifions l'écriture de en utilisant celle-ci. Il ne reste plus à présent qu'à dériver cette nouvelle écriture... Peu de calculs et nous avons trouvé la bonne formule !   Conclusion : la morale de tout cela est qu'il vaut mieux prendre son temps et voir si on ne peut pas simplifier l'écriture d'une fonction avec exponentielle avant de dériver.  Car exp a des propriétés comme ln. L'alternative à cette idée, est bien souvent un résultat inévitablement faux !

Nous avons vu que l'on pouvait alléger notablement le travail en utilisant les propriétés de l'exponentielle dans la dérivation. Avec cette même idée, on peut aussi déterminer certaines limites.

Déterminer trois limites de fonctions avec exponentielles f(x) = e3x+1 / e2x-1 f(x) = e2x - e3x f(x) = (e2x + 3) / (2.ex + 1)

Déterminons la limite lorsque x tend vers + de la fonction f(x) = . On notera que nous avons déjà dérivé cette fonction... Au premier abord, f(x) est une forme indéterminée en +. En effet, lorsque x tend vers + : Nous allons donc devoir innover. En fait, nous allons juste nous servir de ce qui a été fait pour la dérivation avec la méthode "intelligente". Nous allons simplifier l'écriture de f(x). Pour tout réel x, on peut écrire que : Or lorsque x tend vers +, x + 2  s'en va aussi vers +  donc f(x) tend vers +.   Conclusion : la limite lorsque x tend + de f(x) est  +. Pour déterminer la limite d'un produit ou d'un quotient d'exponentielles, il peut être avantageux d'utiliser les propriétés d'exp.

Déterminons la limite lorsque x tend vers + de la fonction  f(x) = e2x - e3x. Comme précédemment, nous nous trouvons en face d'une forme indéterminée en +. En effet, lorsque x tend vers + : f(x) = e2x - e3x = - = Pour trouver cette limite, nous allons devoir modifier l'écriture de f(x). Globalement, deux méthodes permettent de déterminer cette limite. Evoquons-les ! Le "polynôme exponentiel"   Factoriser par le terme le  "plus fort" ! f(x) est une sorte de "polynôme exponentiel". En effet, grâce à la propriété iv, nous pouvons écrire que :  f(x) = e2x - e3x = (ex)2 - (ex)3 La fonction f est la composée : du polynôme P(X) = X2 - X3 de la fonction ex. Or, nous savons déterminer la limite d'un polynôme à l'infini : c'est le terme dominant qui impose sa loi ! Donc lorsque X tend vers +, P(X) va vers -. Ainsi : lorsque x tend vers +, ex  tend vers +. donc  f(x) = P(ex)  tend vers -. Pour savoir quelle est la limite d'une somme ou d'une différence, une technique consiste à factoriser par le terme le "plus fort" (celui dont la croissance est la plus forte). Dans la cas de f(x), il s'agit de e3x. Pour tout réel x, on peut écrire que : Or lorsque x tend vers + : e3x  tend vers + e-x - 1  tend vers -1 car e-x a pour limite 0 donc leur produit f(x) tend vers -.   Conclusion : la limite de f(x) lorsque x tend vers +, est -. Il est parfois intéressant d'appliquer à des sommes ou des différences d'exponentielles des traitements réservés aux polynômes...

Déterminons la limite de la fonction  f(x) =   lorsque x tend vers +. Là encore, lorsque x chevauche vers +,  f(x) devient une forme indéterminée. En effet : Pour déterminer cette limite, il va donc falloir ruser, c'est-à-dire modifier l'écriture de f(x). Il y a deux ruses possibles. Les deux s'inspirent de ce que nous avons déjà fait précédemment ! La "fonction rationnelle exponentielle"   Factoriser haut et bas par leur terme le "plus fort" ! f(x) est quelque part (mais on ignore où) une sorte de "fonction rationnelle exponentielle". En effet grâce à la propriété iv, on a que : La fonction f est la composée : de la fonction rationnelle R(X) = . de la fonction ex. Par bonheur, nous savons déterminer la limite à l'infini d'une fonction rationnelle : il suffit de s'intéresser au quotient des termes dominants. Donc lorsque X tend vers +, R(X) va vers +. Ainsi : lorsque x tend vers +, ex  tend vers +. donc  f(x) = R(ex)  tend vers +. f(x) est en quelque sorte un quotient de titans. Afin de les affaiblir, nous allons factoriser numérateur et dénominateur par leurs termes dominants. Pour le numérateur, il s'agit de e2x. Pour le dénominateur, il s'agit de ex. Pour tout réel x, on peut écrire que : Or lorsque x tend vers + : 1 + 3.e-2x  tend vers 1  car e-2x tend vers 0. 2 + e-x  tend vers 2  car e-x tend vers 0.. donc leur quotient tend vers 1/2. Ainsi lorsque x tend vers +, on a : Donc la limite de f(x) en +, est donc +.   Conclusion : la limite de f(x) lorsque x tend vers +, est +. Il peut être productif d'appliquer à des quotients avec exponentielles des traitements similaires à ceux des fonctions rationnelles...

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) AMLTI Août 2000/Janvier 2003. Tous droits réservés.