| Les puissances sont surtout abordées en Terminale Scientifique. Elles sont un peu élément périphérique du programme. Voilà donc, une bonne raison d'en parler... |


Les puissances sont introduites en quatrième. Mais il ne s'agit là que de puissances entières. En recourant au logarithme népérien et à l'exponentielle, il est possible d'étendre cette notion de puissance.
Et puis il y a le côté fonctionnel : si la variable x est l'exposé, on a alors une fonction puissance. Si elle est l'exposant, on a alors une fonction exponentielle.
Voici donc ce dont nous parlerons dans ce troisième volet de la série il était une fois...
Au commencement.
Au commencement, il y avait la fonction logarithme et sa réciproque : la fonction exponentielle. En combinant les deux, on obtint la puissance réelle...
| Définition de la puissance réelle. x est un réel strictement positif et a est un réel quelconque. xa (appelez-le "x puissance a" ou "x exposant a") est le réel défini par : xa = exp(a . ln(x)) = ea . ln(x) |
Ainsi donc, tout réel strictement positif x peut être élevé à une puissance quelconque. Par exemple, on peut avoir :
 . En effet :
. En effet : 
 . En effet :
. En effet : 
 élevé à la puissance
élevé à la puissance  . En effet :
. En effet : 
 = e
= e . ln(
. ln( )
)Certes, tout cela est assez exotique et quelque peu superficiel mais c'est tout à fait légal !
Une puissance réelle est avant tout une exponentielle. Or une exponentielle est toujours strictement positive. |
La définition de la puissance réelle est 100% compatible avec la puissance entière : celle que nous connaissons... Voyons cela.
Pour tout entier relatif n, nous savons que si x est un réel strictement positif alors n . ln(x) = ln(xn).
Ainsi donc :

Les deux types de puissance sont donc totalement compatibles... mais seulement pour les nombres réels x strictement positifs !
En conclusion, on a donc la chose suivante :
| Puissance entière | Puissance réelle | ||
| Exposant entier positif | x × ...... × x | = xn = | en . ln(x) |
| Exposant entier négatif |  × ...... × × ...... ×  |
= x-n = | e-n . ln(x) |
| Deux produits de n facteurs | x est strictement positif |
De plus, la racine carrée correspond à l'exposant ½.
En effet, pour tout réel strictement positif x, on peut écrire que :
x½ = exp(½ . ln(x)) = exp(ln( )) =
)) =  .
.
C'est là la simple application d'une propriété du logarithme népérien...
| Le problème de l'exposant 0.
Depuis la classe de quatrième, une question est restée sans réponse convaincante: à quoi x0 est-il égal ? Si l'on suit la définition de la puissance entière, il s'agit d'un produit de 0 facteur x !
Beaucoup croient que x0 est égal à 0. Cela leur paraît logique !
x0 = e0 . ln(x) = e0 = 1 Voilà pourquoi en quatrième, on vous dit que x0 est égal à 1. |
Propriétés de la puissance.
A l'instar du logarithme népérien et de l'exponentielle dont elle dérive, la puissance réelle a certaines propriétés : celles de la puissance...
| Propriétés de la puissance réelle. Dans ce qui suit, x et y sont deux réels strictement positifs. a et b sont deux réels quelconques. | ||||
Ainsi donc par exemple :
Toutes ces propriétés vous sont sans doute très familières. Ce sont les mêmes que celles de la puissance entière. Les seules choses qui changent, sont leurs démonstrations. | ||||
| Les preuves de ces six propriétés. Nous l'avons dit et répété : la puissance réelle est une exponentielle de logarithme ! Pour démontrer nos six propriétés, nous allons donc nous servir des propriétés des deux compères.
D'où ces sept propriétés... |
Les fonctions puissances réelles.
Les fonctions "puissances réelles" sont des fonctions que nous noterons fa. On les définit de la manière suivante :
| Définition : a est un réel quelconque.
fa est la fonction puissance (réelle) a. Elle est définie pour tout réel strictement positif x par : fa(x) = xa = ea . ln(x) |
Dans ce paragraphe, nous allons étudier ce genre de fonction. Les hostilités peuvent commencer !
Nous savons qu'une fonction fa est définie sur l'intervalle ]0 ; + [.
[.
Or nous savons que ln est dérivable sur cet intervalle. Comme l'exponentielle est dérivable sur R, nous pouvons dons affirmer que fa(x) = ea . ln(x) est dérivable sur ]0 ; + [.
[.
Comme on peut dériver fa, nous allons donc le faire.
fa étant une fonction composée, nous emploierons la formule prévue à cet effet.
Pour tout réel strictement positif x, on peut écrire que :

Or une puissance réelle est toujours strictement positif. C'est donc a qui donnera son signe à fa'(x).
Pour les variations de fa, nous devons donc envisager deux cas :
| a est négatif | a est positif | |
| Pour tout réel x > 0, on a : fa'(x)
est négatif.
Donc fa est décroissante sur ]0 ; +  [. [. |
Pour tout réel x > 0, on a : fa'(x)
est positif.
Donc fa est croissante sur ]0 ; +  [. [. |
 .
.
Pour déterminer les limites de fa en 0 et + , nous allons utiliser la définition de la puissance réelle.
, nous allons utiliser la définition de la puissance réelle.
En effet, nous savons que pour tout x strictement positif, fa(x) = ea . ln(x).
A l'instar de ce qui s'était passé pour la dérivation, tout dépend de a et de son signe.
Nous devons donc envisager deux cas :
| a est négatif | a est positif | |
| Lorsque x tend vers 0, | ln(x) tend vers - , ,
donc a.ln(x) tend vers +  , ,
donc fa(x) tend vers +  . . |
ln(x) tend vers - , ,
donc a.ln(x) tend vers -  , ,
donc fa(x) tend vers 0. |
| Lorsque x tend vers +¥, | ln(x) tend vers + , ,
donc a.ln(x) tend vers -  , ,
donc fa(x) tend vers 0. |
ln(x) tend vers + , ,
donc a.ln(x) tend vers +  , ,
donc fa(x) tend vers +  . . |
 |
 |
Récapitulons tout ce que nous avons trouvé : voici la conclusion de tout ce travail !
Conclusion : toute fonction fa est dérivable sur ]0 ; + [. De plus, pour tout réel x de cet intervalle : [. De plus, pour tout réel x de cet intervalle :
De plus :
|
Nous avions déjà fait les mêmes observations lorsque nous avions parlé des fonctions puissances entières, racine carré et inverse en Seconde.
Pour compléter cette étude, nous allons faire quelques remarques sur cette conclusion :
 [.
[.
 [ sur ]0 ; +
[ sur ]0 ; + [.
[.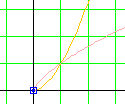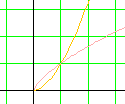 |
Il est donc possible de prolonger par continuité fa en 0 en posant fa(x) = 0.
On pourrait croire cette chose exceptionnelle !
|
 [ de la fonction "puissance entière" xn qui est définie sur ]-
[ de la fonction "puissance entière" xn qui est définie sur ]- ; +
; + [.
[.
 [ de la fonction inverse
[ de la fonction inverse 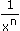 = x-n qui est définie sur ]-
= x-n qui est définie sur ]- ; 0[ È ]0 ; +
; 0[ È ]0 ; + [.
[.| Une des conséquences de la bijectivité des fonctions puissances réelles est ce que l'on appelle les racines n-ième. Pour connaître la vraie vérité vraie sur ce sujet, cliquez sur ce qui suit ! |  |
Les fonctions exponentielles.
Lorsque la variable x est en bas, on est en présence de fonctions puissances. Mais lorsqu'elle est en exposant, on est en face d'une fonction exponentielle... dans une certaine base !
| Définition : a est un réel strictement positif.
L'exponentielle de base a est la fonction notée expa définie pour tout réel x par : expa(x) = ax = ex . ln(a) |
Deux remarques sur cette définition :
Dans la suite de ce paragraphe, nous allons étudier ce genre de fonction !
Comme l'exponentielle est dérivable sur ]- ; +
; + [, alors il en va de même pour toute fonction expa.
[, alors il en va de même pour toute fonction expa.
Pour déterminer la dériver de cette dernière, il suffit d'utiliser la formule de la dérivée de la composée.
Pour tout réel x, on peut donc écrire que :
(expa)'(x) = [x.ln(a)]' . ex.ln(a) = ln(a) . ex.ln(a) = ln(a) . expa(x)
Comme est toujours positif, c'est donc ln(a) qui donnera son signe à la dérivée.
Nous devons donc envisager deux cas :
| ln(a) est négatif ou a < 1 | ln(a) est positif ou a > 1. | |
| Pour tout réel x, (expa)'(x) est négatif.
Donc expa est décroissante sur ]-  ; + ; + [. [. |
Pour tout réel x, (expa)'(x) est positif.
Donc expa est croissante sur ]-  ; + ; + [. [. |
 et en +
et en + .
.
Toute fonction exponentielle de base a ne peut avoir que deux limites : une en - et une autre en +
et une autre en + .
.
Quand on observe la forme "exponentielle" de expa, on devine que tout va dépendre du signe de ln(a).
En effet, on a :
expa(x) = ax = ex . ln(a)
Nous devons donc envisager deux cas comme précédemment.
| ln(a) est négatif ou a < 1 | ln(a) est positif ou a > 1 | |
Lorsque x tend vers - , , |
x . ln(a) tend vers + , ,
donc expa(x) tend vers +  . . |
x . ln(a) tend vers - , ,
donc expa(x) tend vers 0. |
| Lorsque x tend vers +¥, | x . ln(a) tend vers - , ,
donc expa(x) tend vers 0. |
x . ln(a) tend vers + , ,
donc expa(x) tend vers +  . . |
 |
 |
Avec tous ces renseignements, nous pouvons dresser les tableaux de variations des exponentielles de base a.
Nous en profiterons pour dire deux mots sur leurs courbes comme nous l'avons fait avec les fonctions puissances.
Conclusion : toute fonction expa est dérivable sur ]- ; + ; + [. De plus, pour tout réel x : [. De plus, pour tout réel x :
De plus :
|
|||||||||
Les exponentielles de base sont des fonctions strictement monotones (c'est-à-dire toujours croissante ou décroissante). Ce sont donc des bijections.
Mais qui dit bijection, dit réciproque ! Ce qui suit essaiera de répondre à cette question.
| La réciproque des exponentielles de base a.
Comme la fonction expa est strictement monotone sur ]-  ; + ; + [, c'est donc une bijection de cet intervalle sur ]0 ; + [, c'est donc une bijection de cet intervalle sur ]0 ; + [. [.
Nous allons essayer de déterminer sa réciproque. Pour y parvenir, il n'y a pas cinquante mille moyens, il faut faire ce qui suit : Soit y un réel de l'intervalle ]0 ; +
|
| Il était une fois... la puissance réelle : l'essentiel |  |