 |
Complexitudes 3/3 : algébriquement |
Résolution d'équations ...complexes.
Globalement une équation complexe se résout à peu de choses près comme une équation réelle. Sauf que parfois on va plus au fond des choses...
Voyons cela sur quelques exemples :
Et ça commence maintenant !
 |
 |
 |
| |
Résolution d'équations du premier degré.
Dans les grandes lignes, une équation du premier degré à coefficients complexes se résout comme une avec des réels. Voyons cela sur un exemple.
Résolvons dans l'équation (4 + 7.i).z + 5 = 2 - 3.i .
Globalement il y a deux méthodes : la brutale et la délicate.
| la méthode brutale |
|
la méthode délicate |
 est un corps. On peut donc y manoeuvrer comme dans est un corps. On peut donc y manoeuvrer comme dans
 . .

|
|
Au lieu de résoudre une équation complexe, nous allons en faire deux réelles.
Pour cela, on pose z = x + i.y
L'inconnue complexe est devenue une double inconnue réelles.

Or deux nombres complexes sont égaux si et seulement si leurs parties réelles et imaginaires le sont. Ainsi, on arrive au système 2×2:

Il ne reste plus qu'à le résoudre ! |
Conclusion : l'unique solution de cette équation est -
 + +
 i. i.
Note : les deux méthodes ont leurs avantages. Mais celle des seigneurs est certainement la première ! |
| |
 |
 |
 |
 |
 |
 |
| |
Résolution d'équations du second degré
Dans  certaines équations du second degré n'admettent pas de solutions. C'est le cas lorsque leur discriminant est négatif. certaines équations du second degré n'admettent pas de solutions. C'est le cas lorsque leur discriminant est négatif.
Si on recherche les solutions dans 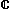 alors il en va différemment. alors il en va différemment.
La théorie : nous savons depuis la première qu'une équation du second degré a.x2 + b.x + c = 0 n'admet des solutions que lorsque son discriminant n'est pas négatif.
Revenons sur ce discriminant !Le discriminant est introduit lors d'une factorisation, lors de du raisonnement suivant :

Pour poursuivre la factorisation, il faut alors pouvoir trouver une racine carrée à
 . .
Dans  , celle-ci n'existe que si , celle-ci n'existe que si
 n'est pas négatif. D'où l'absence de solutions. n'est pas négatif. D'où l'absence de solutions.
Par contre dans  , les choses sont différentes. , les choses sont différentes. En effet, si
 est négatif alors il existe deux nombres complexes dont le carré est est négatif alors il existe deux nombres complexes dont le carré est
 . .
Il s'agit de i. et de -i. et de -i. . .
Dans  , même lorsque le discriminant , même lorsque le discriminant
 est négatif, il est donc possible de poursuivre la factorisation engagée en utilisant l'identité remarquable a2 - b2. est négatif, il est donc possible de poursuivre la factorisation engagée en utilisant l'identité remarquable a2 - b2.
Ainsi lorsque
 est négatif, on peut écrire que : est négatif, on peut écrire que :

Il est alors facile d'en déduire les deux solutions complexes de l'équation a.x2 + b.x + c = 0.
En résumé, il faut donc retenir que :
Fort de cela, il est alors possible de résoudre n'importe quelle équation. |
La pratique : Résolvons dans
 l'équation x2 - 4.x + 13 = 0. l'équation x2 - 4.x + 13 = 0.
Commençons par calculer son déterminant
 . .
 = (-4)2 - 4 × 1 × 13 = 16 - 52 = -36 = (-4)2 - 4 × 1 × 13 = 16 - 52 = -36
Comme
 est négatif donc l'équation admet deux solutions complexes en la personne : est négatif donc l'équation admet deux solutions complexes en la personne :

Les deux solutions complexes de cette équation sont les conjugués l'une de l'autre. Il en va ainsi pour chaque équation du second degré à coefficients réels.
De plus, on peut écrire que :
P(z) = z2 - 4.z + 13 = (z - 2 + 3i) . (z - 2 - 3i)
C'est là la forme factorisée du polynôme P dans
 . .
Par contre, ce polynôme P est irréductible (ne peut pas être factorisé) sur
 . . |
Juste un peu plus loin : Jusqu'à présent, les coefficients des équations que nous avons eu à résoudre étaient réels. Voyons ce que cela donne lorsqu'ils sont complexes.
Résolvons dans l'équation z2 + (3+2i) . z + (5+i) = 0.Ici encore, il convient de calculer le discriminant
 car ce que nous avons repris précédemment convient. car ce que nous avons repris précédemment convient.
En effet, tout repose sur le fait de trouver une racine carrée à
 . Ce qui dans . Ce qui dans
 est toujours possible. est toujours possible.
 = b2 - 4.a.c = (3+2i)2 - 4 × 1 × (5+i) = -15 + 8i = b2 - 4.a.c = (3+2i)2 - 4 × 1 × (5+i) = -15 + 8i
Il s'agit à présent de trouver une racine carrée à notre discriminant. Autrement dit, une racine seconde de
 . .
L'offensive peut alors continuer. Notre équation initiale admet alors deux solutions :
Comme quoi, il n'est pas très difficile de résoudre des équations du second degré à coefficients complexes ! C'est juste un peu long !
Ainsi on peut écrire que :
P(z) = z2 + (3+2i) . z + (5+i) = (z + 2 + 3i) . (z + 1 - i)
Ce polynôme P est donc entièrement factorisable dans  . .
|
| |
 |
 |
 |
 |
 |
 |
| |
Résolution d'une équation du troisième degré.
Factoriser dans  un polynôme du troisième degré à coefficients réels est à la portée de tout bon élève de Première. un polynôme du troisième degré à coefficients réels est à la portée de tout bon élève de Première.
Le même travail sur 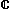 ne pose guère plus de difficultés. Tout au plus y a-t-il un peu plus de calculs... ne pose guère plus de difficultés. Tout au plus y a-t-il un peu plus de calculs...
| L'énoncé : On considère le polynôme P(z) = z3 + (-5 + i).z2 + (17 - 4i).z + (-13 + 13i)
a) Démontrer que 1 - i est une racine de P(z).
b) En déduire la résolution de l'équation P(z) = 0. |
| La réponse :
a) Pour prouver que 1 - i est une racine de P, il suffit de calculer P(1 - i).
| P(1 - i) | = (1 - i)3 + (-5 + i) . (1 - i)2 + (17 - 4i) . (1 - i) + (-13 + 13i) |
| = (-2 - 2i) + (-5 + i) . (-2i) + (17 - 4i) . (1 - i) + (-13 + 13i) |
| = (-2 - 2i) + (2 + 10i) + (13 - 21i) + (-13 + 13i) = 0 | Donc 1 - i est une racine du polynôme P.
b) Pour résoudre cette équation, il faut procéder comme nous l'aurions fait avec n'importe quel polynôme à coefficients réels : nous devons factoriser...
Comme 1 - i est une racine du polynôme P, alors il est factorisable par (z - 1 + i).
Pour effectuer cette tache, on dispose des mêmes méthodes que pour les polynômes réels. A savoir :
Adepte de l'efficacité et de la puissance, nous opterons pour cette dernière.
Pour factoriser P par (z - 1 + i), nous devons donc le diviser par (z - 1 + i).

Ainsi pour tout nombre complexe z, P(z) = (z - 1 + i) . (z2 - 4.z + 13).
Pour achever la manoeuvre, il reste à "casser" z2 - 4.z + 13.
Mais nous ne referons pas ce qui nous a déjà causé du tracas. En effet, nous savons depuis le précédent exercice que z2 - 4.z + 13 = (z - 2 + 3i) . (z - 2 - 3i).
Pour tout nombre complexe z, on peut donc écrire que :
P(z) = (z - 1 + i) . (z - 2 + 3i) . (z - 2 - 3i)
| Conclusion : L'équation P(z) = 0 admet donc trois solutions : 1 - i, 2 - 3i et 2 + 3i. |
|
| |
 |
 |
 |
La morale de ces trois exercices est que dans
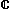 , tous les polynômes P(z) qu'ils soient à coefficients complexes ou réels
sont entièrement factorisables. C'est-à-dire que :
, tous les polynômes P(z) qu'ils soient à coefficients complexes ou réels
sont entièrement factorisables. C'est-à-dire que :

C'est là l'illustration du théorème d'Alembert-Gauss :
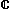 est un corps algébriquement clos c'est-à-dire que tous les polynômes complexes admettent au moins une racine dans
est un corps algébriquement clos c'est-à-dire que tous les polynômes complexes admettent au moins une racine dans
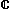 . Même ceux qui sont irréductibles dans
. Même ceux qui sont irréductibles dans
 .
.
Au-delà de 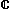 : les quaternions.
: les quaternions.
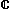 est un corps
quasi-parfait. En effet comme nous venons de le voir, tout polynôme y est totalement scindé. La question que l'on peut se poser est :
est un corps
quasi-parfait. En effet comme nous venons de le voir, tout polynôme y est totalement scindé. La question que l'on peut se poser est :

Existe-t-il quelque chose au-delà des nombres complexes qui soit comparable du point de vue des opérations à
 et à
et à
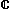 ? Autrement écrit, un corps au-delà de
? Autrement écrit, un corps au-delà de
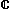 ?
?
La réponse est oui ! Mais à la différence des deux précédents, il n'est pas commutatif pour la multiplication. C'est-à-dire que le produit a × b peut être différent du produit b × a.
Ce corps est celui des quaternions. On le note
 . On doit sa
genèse à l'irlandais William Hamilton au XIXème siècle.
. On doit sa
genèse à l'irlandais William Hamilton au XIXème siècle.
Pour le définir, il convient d'introduire deux nouveaux nombres j et k.
Puis on construit une table de multiplication :
Produit de
a × b |
i |
j |
k |
| i |
-1 |
k |
-j |
| j |
-k |
-1 |
i |
| k |
j |
-i |
-1 |
Avec cette table, l'ensemble  se retrouve muni d'une structure de corps.
se retrouve muni d'une structure de corps.
Tout quaternion est alors de la forme réel1 + réel2 i + réel3 j + réel4 k.
Mais tout cela est une autre histoire...
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par
la taverne de l'Irlandais.
(c) AMLTI Janvier 2001/Janvier 2003. Tous droits réservés.



![]() , tous les polynômes P(z) qu'ils soient à coefficients complexes ou réels
sont entièrement factorisables. C'est-à-dire que :
, tous les polynômes P(z) qu'ils soient à coefficients complexes ou réels
sont entièrement factorisables. C'est-à-dire que :
![]() est un corps algébriquement clos c'est-à-dire que tous les polynômes complexes admettent au moins une racine dans
est un corps algébriquement clos c'est-à-dire que tous les polynômes complexes admettent au moins une racine dans
![]() . Même ceux qui sont irréductibles dans
. Même ceux qui sont irréductibles dans
![]() .
.![]() : les quaternions.
: les quaternions.
![]() est un corps
quasi-parfait. En effet comme nous venons de le voir, tout polynôme y est totalement scindé. La question que l'on peut se poser est :
est un corps
quasi-parfait. En effet comme nous venons de le voir, tout polynôme y est totalement scindé. La question que l'on peut se poser est :
![]() et à
et à
![]() ? Autrement écrit, un corps au-delà de
? Autrement écrit, un corps au-delà de
![]() ?
?![]() . On doit sa
genèse à l'irlandais William Hamilton au XIXème siècle.
. On doit sa
genèse à l'irlandais William Hamilton au XIXème siècle.
![]() se retrouve muni d'une structure de corps.
se retrouve muni d'une structure de corps.