Au sommaire : Sommes et différences Produits Fractions

Dans cette page, nous allons aborder les différentes techniques qui permettent de simplifier des expressions avec racines carrées. Le tout au travers de huit missions... 

Missions :     une    deux    trois    quatre    cinq    six    sept   huit

 

Simplifier des sommes et des différences.
Comme chacun est désormais sensé le savoir, la racine et l'addition sont incompatibles. Pour simplifier une somme ou une différence de deux racines, il faut donc se montrer plus astucieux. Ainsi que nous le verrons. Et comme nous le ferons..

Mission Première : écrire   sous la forme a × où a est un entier.

Analysons le problème :

  • Au départ, il y a la racine carrée d'un nombre.
  • A l'arrivée, il y a un produit d'un entier par une racine.

Autrement dit, en utilisant la propriété multiplicative de la racine, il va falloir faire éclore 2 dans 50.
Et comme par hasard, 50 = 25 × 2. Ainsi :
 
Mission seconde : écrire sous la forme  a × où a est un entier.

Comme la racine est incompatible avec la soustraction comme avec l'addition, il est hors de question de faire :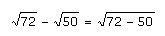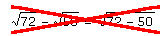

Ce que nous allons faire, c'est nous inspirer de la mission première. Nous allons convertir et en .

 

Simplifier des produits.
Même la racine carrée se marie bien avec la multiplication, on ne peut pas faire tout et n'importe quoi.
Comme nous le verrons, le calcul sur les racines s'apparente énormément à celui sur les x.

Mission troisième :  écrire ×   sous la forme a. où a est un entier.

Le produit des racines est la racine du produit. Telle est la règle...
Nous allons essayer de l'appliquer intelligemment.
On peut écrire que :
 
Mission quatrième : écrire × (3. - 1)  sous la forme a + b. où a et b sont des entiers.

Les sont comme les x : on ne peut pas les éliminer, on est obligé de composer avec eux...
Et bien justement, développons l'expression  × (3. - 1)  comme si nous avions des x à la place des .
Ainsi :
 
Mission cinquième : écrire × (2. - 1)  sous la forme a + b. où a et b sont des entiers.

Cette mission ressemble à la précédente : nous allons donc développer l'expression qui nous est proposée. Et après, nous verrons...
Ainsi :
 
Mission sixième : écrire (2. - 1)2  sous la forme c + d. où a et b sont des entiers.

Nous avons dit dans la quatrième mission que le calcul sur les racines ressemblait à celui sur les x.
Si  nous avions eu A = (2. - 1)2, nous aurions développer cette expression en utilisant l'identité remarquable.

(a - b)2 = a2 - 2.a.b + b2 

Et bien c'est ce que nous allons faire avec notre expression. Dans le présent cas, nous aurons :

a = 2.    et    b = 1
Ainsi :

 
Mission septième :  écrire ()5   sous la forme a. où a est un entier.

Certains diront qu'il s'agit là de la puissance d'une racine et non d'un produit.
Sauf que la puissance est une façon commode et économique de noter un produit d'un nombre par lui-même.
Par conséquent, on peut écrire que :

 

Simplifier des fractions.
Nous l'avons déjà dit à qui voulait l'entendre : la racine laisse passer la multiplication et la division. Autrement dit, elle autorise certaines choses sur les fractions...
Les mathématiciens, grands esthètes s'il en est, n'aiment pas laisser des racines carrées au dénominateur d'une fraction. Manie de vieux grincheux ? Quoiqu'il en soit, sous certaines conditions, il est possible d'arriver à les satisfaire...

Mission huitième : écrire   sous la forme a. où a est une fraction.

Analysons le problème : il s'agit d'éliminer du dénominateur .
Or, nous savons que × = 7.
Autrement dit, en multipliant le numérateur et le dénominateur de la fraction, nous allons pouvoir faire aboutir notre rêve. Ainsi :

Il existe d'autres techniques permettant de simplifier des fractions avec racine carrée au dénominateur. L'une d'elle s'appelle la quantité conjuguée. Mais tout cela est une autre histoire...

Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par la taverne de l'Irlandais.
(c) Avril 2000/Janvier 2003. Tous droits réservés.