Cliquer ici pour cacher les solutions.
a)
Pour tracer les droites D et  , il nous
faut connaître deux de leurs points. La forme de leurs équations
cartésiennes indique que D et
, il nous
faut connaître deux de leurs points. La forme de leurs équations
cartésiennes indique que D et  coupent
les axes.
coupent
les axes.
Lorsqu'une droite est parallèle à l'un des axes (abscisses
ou ordonnées) alors son équation cartésienne est soit
de la forme a.x + c = 0 ou bien de la forme b.y + c = 0. Ce n'est ni le
cas pour D, encore moins pour  .
.
Ainsi l'une comme l'autre comportent des points dont les abscisses
ou les ordonnées sont nulles. En effet, tout point de l'axe des
abscisses (l'axe horizontal) a une ordonnée nulle. De même,
tout point de l'axe des ordonnées (l'axe vertical) a une abscisse
nulle.
Pour D :
- Si x = 0 alors –2.y = -28 c'est-à-dire y = 14. La droite D coupe l'axe des ordonnées en (0 ; 14).
- Si y = 0 alors 10.x = -28 c'est-à-dire x = -2,8. La droite D coupe l'axe des abscisses en (-2,8 ; 0).
Pour  :
:
- Si x = 0 alors y = 18/5 = 3,6. La droite
 coupe l'axe des ordonnées en (0 ; 3,6).
coupe l'axe des ordonnées en (0 ; 3,6).
- Si y = 0 alors x = 18. La droite
 coupe l'axe des abscisses en (18 ; 0).
coupe l'axe des abscisses en (18 ; 0).
Ayant deux points pour chacune des droites, nous pouvons faire notre la figure.
b) Avant d'aller plus loin, calculons
les coordonnées de certains vecteurs. Ainsi nous saurons désormais
que : 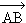 (-4 ; 1),
(-4 ; 1), 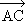 (-1
; -5) et
(-1
; -5) et 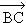 (-3 ; -6).
(-3 ; -6).
Pour voir si le triangle (ABC) est rectangle en A, il y a quatre
cheminements possibles :
- Utiliser le théorème
de Pythagore. Il faut alors calculer
AB2, AC2 et BC2.
Connaissant les coordonnées des vecteurs correspondants, il
vient que :
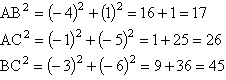 Comme AB2 + AC2 = 43 et que BC2 = 45,
le triangle (ABC) n'est donc pas rectangle en A.
Comme AB2 + AC2 = 43 et que BC2 = 45,
le triangle (ABC) n'est donc pas rectangle en A.
- Utiliser le test
d'orthogonalité de deux vecteurs sur
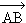 et
et 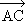 . C'est certainement
la solution la plus rapide.
. C'est certainement
la solution la plus rapide.
Comme (-4) ´ (-1) + 1 ´
(-5) = -1, les vecteurs 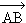 et
et 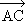 ne sont pas orthogonaux.
Donc le triangle (ABC) n'est pas rectangle en A.
ne sont pas orthogonaux.
Donc le triangle (ABC) n'est pas rectangle en A.
- Déterminer une équation
cartésienne pour les droites (AB) et (BC), puis utiliser le test
de perpendicularité sur les équations
cartésiennes. C'est la solution la plus longue.
Un vecteur directeur de la droite (AB) qui passe par A(2 ; 3), est 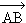 (-4
; 1). On détermine alors
une équation cartésienne de cette droite. Il s'agit de :
x + 4.y – 14 = 0.
(-4
; 1). On détermine alors
une équation cartésienne de cette droite. Il s'agit de :
x + 4.y – 14 = 0.
De la même manière, (AC) qui passe par A, admet est 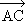 pour vecteur directeur. Une équation
cartésienne est donc : -5.x + y + 7 = 0.
pour vecteur directeur. Une équation
cartésienne est donc : -5.x + y + 7 = 0.
Ayant deux équations cartésiennes, on peut utiliser le
test :
1 ´ (-5) + 4 ´
1 = -1 ¹ 0
Les droites (AB) et (AC) n'étant pas perpendiculaires, le triangle
(ABC) n'est donc pas rectangle en A.
- Déterminer les coefficients
directeurs des droites (AB) et (AC), puis utiliser le test
de perpendicularité sur ceux-ci (leur produit doit être égal
à -1).
Comme les points A et B n'ont pas même abscisse, on peut calculer
le coefficient directeur m(AB) de la droite (AB). Il en va de
même pour m(AC). Ainsi :
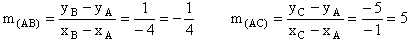 Et finalement :
Et finalement :
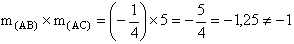 Les droites (AB) et (AC) ne sont donc pas perpendiculaires. Par conséquent,
le triangle (ABC) n'est pas rectangle en A.
Les droites (AB) et (AC) ne sont donc pas perpendiculaires. Par conséquent,
le triangle (ABC) n'est pas rectangle en A.
c) Nous connaissons une équation cartésienne
de la droite D et un vecteur directeur de (AC). Pour voir si ces deux droites
sont parallèles, deux possibilités sont à envisager
:
- On détermine une équation
cartésienne de (AC), puis on applique le test de parallélisme
correspondant.
La droite (AC) qui passe par A(2 ; 3), admet 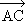 (-1
; -5) pour vecteur directeur. On détermine
alors une équation cartésienne de cette droite. -5.x + y
+ 7 = 0.
(-1
; -5) pour vecteur directeur. On détermine
alors une équation cartésienne de cette droite. -5.x + y
+ 7 = 0.
En appliquant le test sur les deux équations connues, il vient
que :
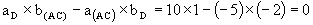 Les droites D et (AC) sont donc parallèles.
Les droites D et (AC) sont donc parallèles.
- on détermine un vecteur directeur
de la droite D et l'on regarde s'il est colinéaire à un vecteur
directeur de (AC) grâce au déterminant.
Comme 10.x – 2.y +28 = 0 est une équation cartésienne
de D, un vecteur directeur de cette
droite est le vecteur 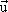 (2
; 10). Regardons si ce vecteur est colinéaire à
(2
; 10). Regardons si ce vecteur est colinéaire à  .
.
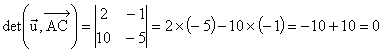 Ces deux vecteurs directeurs sont donc colinéaires. En conséquence,
D et (AC) sont parallèles.
Ces deux vecteurs directeurs sont donc colinéaires. En conséquence,
D et (AC) sont parallèles.
Là encore, pour répondre à
la question, deux cheminements sont possibles;
On peut montrer qu'elles sont perpendiculaires
à partir de leurs équations cartésiennes.
Nous savons qu'une équation cartésienne de la droite
(AC) est -5.x + y + 7 = 0.
Une équation de  est x + 5.y –18
= 0. On applique le test de
perpendicularité correspondant.
est x + 5.y –18
= 0. On applique le test de
perpendicularité correspondant.
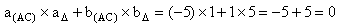 Les droites (AC) et
Les droites (AC) et  sont donc perpendiculaires.
sont donc perpendiculaires.
On peut montrer qu'un vecteur directeur
de l'une est orthogonal à un vecteur directeur de l'autre.
x + 5.y – 18 = 0 étant une équation cartésienne
de  , un vecteur
directeur de cette droite est le vecteur
, un vecteur
directeur de cette droite est le vecteur 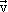 (5
; -1). Regardons si ce vecteur est orthogonal à
(5
; -1). Regardons si ce vecteur est orthogonal à 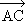 (-1
; -5) avec notre test.
5 ´ (-1) + (-1) ´
(-5) = -5 + 5 = 0
Donc les vecteurs
(-1
; -5) avec notre test.
5 ´ (-1) + (-1) ´
(-5) = -5 + 5 = 0
Donc les vecteurs 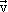 et
et 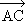 sont orthogonaux. Par conséquent, les droites
sont orthogonaux. Par conséquent, les droites  et (AC) sont perpendiculaires.
et (AC) sont perpendiculaires.
Pour vérifier qu'un point appartient à
une droite dont on connaît une équation, il suffit de remplacer
x et y par les coordonnées de ce point.
Pour la droite D, on remplace dans le premier membre x et y par –2
et 4 et on regarde ce qui passe :
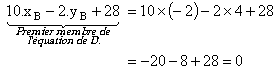 Comme ses coordonnées vérifient son équation cartésienne,
le point B fait donc partie de la droite D.
Comme ses coordonnées vérifient son équation cartésienne,
le point B fait donc partie de la droite D.
De même pour la droite  :
:
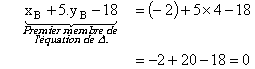 Donc B fait aussi partie de la droite
Donc B fait aussi partie de la droite  .
.
d) Il s'agit là d'une question de cours.
Si G est le centre de gravité de (ABC) alors 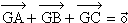 .
.
La relation vectorielle précédente
va nous permettre de trouver les coordonnées de G.
Si on appelle (xG ; yG) les coordonnées
de G alors 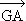 (xG
– 2 ; yG – 3),
(xG
– 2 ; yG – 3), 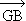 (xG
+ 2 ; yG – 4) et
(xG
+ 2 ; yG – 4) et 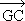 (xG
– 1 ; yG + 2).
(xG
– 1 ; yG + 2).
Donc 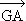 +
+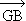 +
+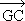 a pour coordonnées
a pour coordonnées
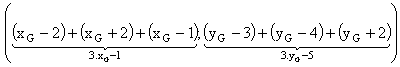 Or le vecteur
Or le vecteur 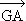 +
+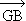 +
+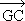 est égal au vecteur nul. L'un et l'autre ont donc des coordonnées
égales. Ainsi :
est égal au vecteur nul. L'un et l'autre ont donc des coordonnées
égales. Ainsi :
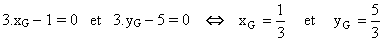 Le point G a donc pour coordonnées (1/3 ; 5/3).
Le point G a donc pour coordonnées (1/3 ; 5/3).
Le centre de gravité étant le point d'intersection
des médianes du triangle (ABC), on aurait pu déterminer les
coordonnées de G en déterminant une équation cartésienne
pour deux de celle-ci. Il aurait suffi ensuite d'en rechercher le point
d'intersection (résolution d'un système). Cependant cette
solution est nettement plus longue...
Le centre de gravité d'un triangle est le point
de concours de ses médianes. Celle issue de C passe donc aussi par
G.
La médiane issue de C est la droite (GC) dont un vecteur directeur
est 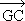 (2/3 ; -11/3).
(2/3 ; -11/3).
Connaissant un de ses points (par exemple C) et l'un de ses vecteurs
directeurs, on détermine sans peine l'une de ses équations
cartésiennes. Par exemple (après simplification) : 11.x +2.y
- 7 = 0.
e) La hauteur issue de A est la droite qui passe
par ce point et qui est perpendiculaire à la droite (BC). Pour déterminer
une équation cartésienne de cette hauteur, nous allons recourir
à l'un de ses vecteurs normaux.
On appelle  ' la hauteur du triangle (ABC)
issue de A. Comme
' la hauteur du triangle (ABC)
issue de A. Comme  ' est perpendiculaire à
la droite (BC), le vecteur
' est perpendiculaire à
la droite (BC), le vecteur 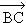 (3
; -6) est donc un vecteur normal de
(3
; -6) est donc un vecteur normal de  '.la hauteur
issue de A.
'.la hauteur
issue de A.
Connaissant un de ses points (à savoir A) et un de ses vecteurs
normaux, on peut déterminer
une équation cartésienne de  '. On trouve : x – 2.y + 4 = 0.
'. On trouve : x – 2.y + 4 = 0.
L'orthocentre est le point de concours des hauteurs
d'un triangle. Théoriquement, pour trouver ses coordonnées,
il suffit de connaître une équation cartésienne de
deux de ces hauteurs. Comme nous connaissons déjà une équation
de  ', il faudrait donc déterminer une
équation de la hauteur passant par B ou de celle issue de C. En
fait, on s'en passait. Explications :
', il faudrait donc déterminer une
équation de la hauteur passant par B ou de celle issue de C. En
fait, on s'en passait. Explications :
On appelle (xH ; yH) les coordonnées du
point H.
Au c, nous avons démontré que les droites
(AC) et  étaient perpendiculaires. Nous
avons aussi vérifié que B appartenait à
cette droite
étaient perpendiculaires. Nous
avons aussi vérifié que B appartenait à
cette droite  . Celle-ci est donc la hauteur
issue de B dans le triangle (ABC).
. Celle-ci est donc la hauteur
issue de B dans le triangle (ABC).
H est donc le point d'intersection des droites  et
et  '. Ses coordonnées vérifient
leurs équations cartésiennes. Ainsi :
'. Ses coordonnées vérifient
leurs équations cartésiennes. Ainsi :
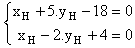 Il suffit alors de résoudre ce système.
On trouve alors que H(16/7 ; 22/7).
Il suffit alors de résoudre ce système.
On trouve alors que H(16/7 ; 22/7).
Cliquer ici pour cacher les solutions.
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par
la taverne de l'Irlandais.
(c) AMLTI Juillet 1998/Janvier 2003. Tous droits réservés.

 .
.
 , il nous
faut connaître deux de leurs points. La forme de leurs équations
cartésiennes indique que D et
, il nous
faut connaître deux de leurs points. La forme de leurs équations
cartésiennes indique que D et  coupent
les axes.
coupent
les axes.
 .
.
 :
: coupe l'axe des ordonnées en (0 ; 3,6).
coupe l'axe des ordonnées en (0 ; 3,6). coupe l'axe des abscisses en (18 ; 0).
coupe l'axe des abscisses en (18 ; 0).![]() (-4 ; 1),
(-4 ; 1), ![]() (-1
; -5) et
(-1
; -5) et ![]() (-3 ; -6).
(-3 ; -6).
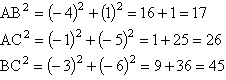
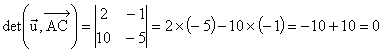
 est x + 5.y –18
= 0. On applique le test de
perpendicularité correspondant.
est x + 5.y –18
= 0. On applique le test de
perpendicularité correspondant.
 sont donc perpendiculaires.
sont donc perpendiculaires. , un vecteur
directeur de cette droite est le vecteur
, un vecteur
directeur de cette droite est le vecteur  et (AC) sont perpendiculaires.
et (AC) sont perpendiculaires.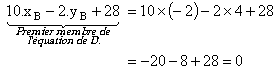
 :
:
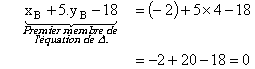
 .
.
![]() .
.
![]() (xG
– 2 ; yG – 3),
(xG
– 2 ; yG – 3), ![]() (xG
+ 2 ; yG – 4) et
(xG
+ 2 ; yG – 4) et ![]() (xG
– 1 ; yG + 2).
(xG
– 1 ; yG + 2).
![]() +
+![]() +
+![]() a pour coordonnées
a pour coordonnées
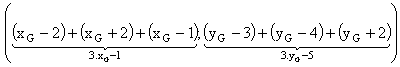
![]() (2/3 ; -11/3).
(2/3 ; -11/3).
 ' la hauteur du triangle (ABC)
issue de A. Comme
' la hauteur du triangle (ABC)
issue de A. Comme  ' est perpendiculaire à
la droite (BC), le vecteur
' est perpendiculaire à
la droite (BC), le vecteur ![]() (3
; -6) est donc un vecteur normal de
(3
; -6) est donc un vecteur normal de  '.la hauteur
issue de A.
'.la hauteur
issue de A.
 '. On trouve : x – 2.y + 4 = 0.
'. On trouve : x – 2.y + 4 = 0.
 ', il faudrait donc déterminer une
équation de la hauteur passant par B ou de celle issue de C. En
fait, on s'en passait. Explications :
', il faudrait donc déterminer une
équation de la hauteur passant par B ou de celle issue de C. En
fait, on s'en passait. Explications :
 étaient perpendiculaires. Nous
avons aussi vérifié que B appartenait à
cette droite
étaient perpendiculaires. Nous
avons aussi vérifié que B appartenait à
cette droite  . Celle-ci est donc la hauteur
issue de B dans le triangle (ABC).
. Celle-ci est donc la hauteur
issue de B dans le triangle (ABC).
 et
et  '. Ses coordonnées vérifient
leurs équations cartésiennes. Ainsi :
'. Ses coordonnées vérifient
leurs équations cartésiennes. Ainsi :