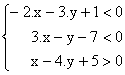1°) Partition du plan par une droite.
C'est une évidence de dire cela, mais une droite partage un plan en deux ! Mais si une droite peut être caractérisée par une équation (de droite), les deux demi-plans peuvent l'être avec des inéquations...C'est ce que montre le théorème suivant !
L'applette suivante illustre le théorème :
Applette illustrant la partition du plan par une droite.
Quelques remarques :
Pour tous les points M(x ; y) d'un même demi-plan, l'expression a.x + b. y + c garde le même signe. Ainsi si pour un point quelconque de ce demi-plan, l'expression est positive alors elle est positive pour tous les autres points de celui-ci. Et elle sera négative sur l'autre demi-plan.
Pour associer à chaque demi-plan le signe qui lui correspond, une bonne astuce consiste à regarder l'origine O(0 ; 0) car alors a.x + b. y + c = c...
Le signe de c donne le signe du demi-plan auquel O appartient.
Et quand O appartient à la droite, et bien on choisit un autre point !
L'ensemble des points M(x ; y) pour lesquels l'expression a.x + b.y + c est nulle est la droite D.
Deux équations cartésiennes peuvent se rapporter à une même droite.
C'est par exemple le cas de x – y + 1 = 0 et y – x –1 = 0 qui sont deux équations de la droite D.
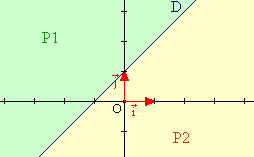
Cette droite partage le plan en deux demis-plan : |
|
2°) Résolutions graphiques de quelques systèmes d'inéquations.
Une applette aide à la résolution des ces systèmes.
Un exemple de résolution de deux inéquations.
Il s'agit de déterminer graphiquement l'ensemble des points M(x ; y) vérifiant ce système. Pour cela, nous utiliserons ce que nous avons fait au paragraphe précédent. La résolution est l'animation ci-dessous.
Un exemple de résolution de trois équations.
La nouveauté outre le nombre d'inéquations (trois au lieu d'une paire), c'est l'"inférieur ou égal" de la première inéquation. Passons à la résolution !
Première inéquation x + 2.y – 2 
0.
 | La droite D passe par les points de coordonnées (0 ; 1) et (2 ; 0).
|
Seconde inéquation 5.x – 4.y – 24 < 0.
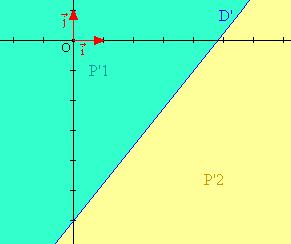 | La droite D' passe par les points de coordonnées (0 ; -6) et (4 ; -1).
|
Dernière inéquation 3.x + y + 4 < 0.
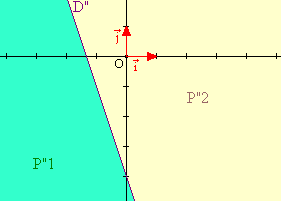 | La droite D" passe par les points de coordonnées (-1 ; -1) et (0 ; -4).
|
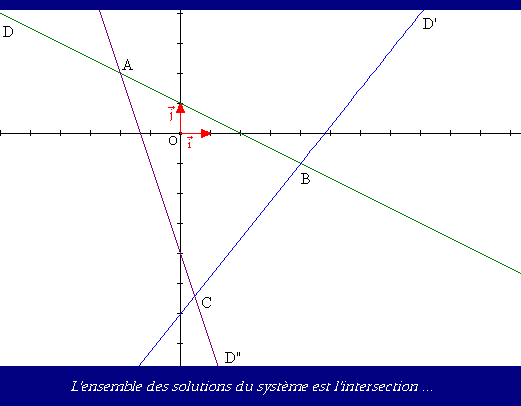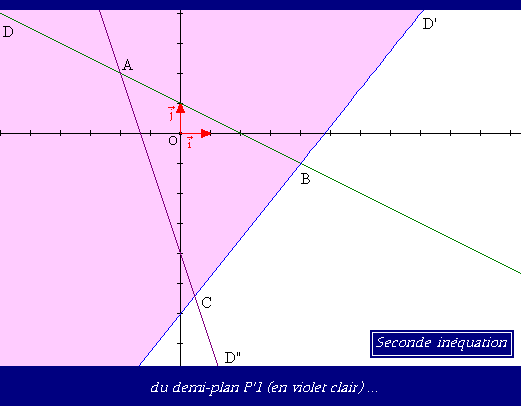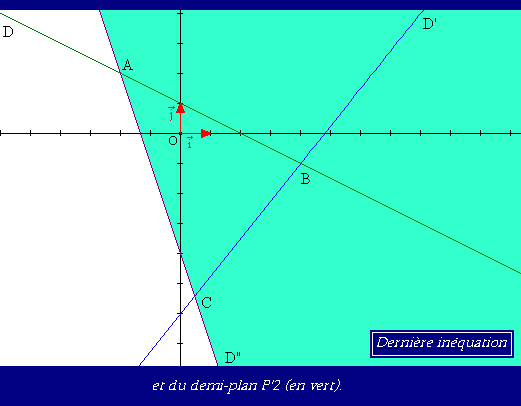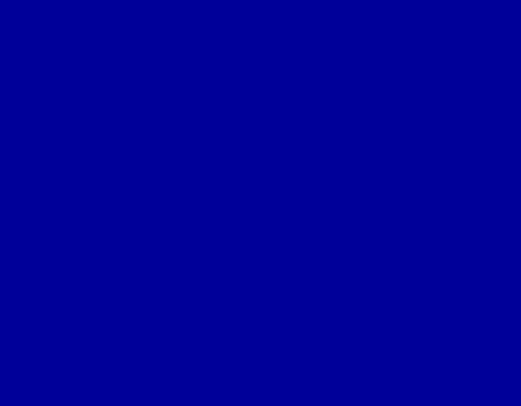
Il ne nous reste plus qu'à récapituler tout cela.
Une remarque :
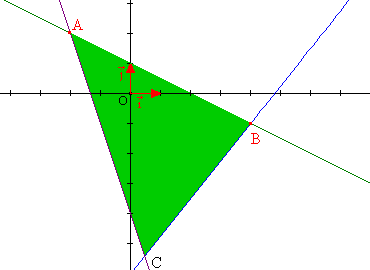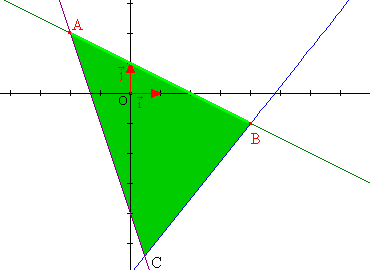
L'ensemble des points solutions du système est l'intérieur du triangle (ABC) et le segment ]AB[ (comprenez le segment sans ses extrémités. C'est comme pour les intervalles).
Si nous devons rajouter ce coté du triangle, c'est à cause de la première inéquation. Le "
0" veut dire inférieur ou égal à 0. L'expression x + 2.y – 2 est inférieure à 0 sur le demi-plan P1 et y est égale sur la droite D (qui est aussi la droite (AB) ).
Si nous devons exclure le point A , c'est parce qu'il ne fait pas partie de P"2. En effet, il se trouve sur D".
Quant à B, il ne fait pas partie de P'1.
3°) Le problème réciproque : caractérisation d'une région du plan par un système.
Nous venons de voir comment résoudre graphiquement un système d'inéquations. Dans ce paragraphe, nous allons faire exactement l'inverse !
|
Enoncé : |  |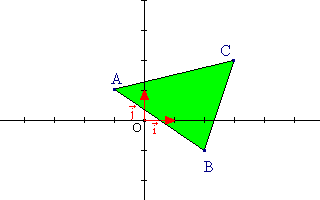
La réponse :
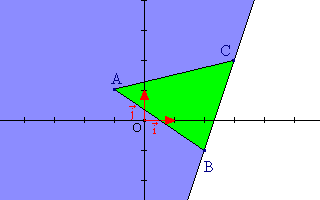
Comme nous l'avons vu dans l'exercice précédent, un triangle est l'intersection de trois demi-plans. Chacun d'entre eux est délimité par un côté de ce polygone. Il nous faut donc déterminer trois inéquations : une pour chaque demi-plan.
|
|
 |
|
|
 |
|
|
 |
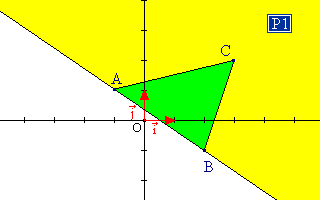La conclusion :
L'intérieur du triangle (ABC) est l'intersection des demi-plans P1, P2 et P3. Celui-ci est solution du système d'inéquations linéaires :
