| Définition : (sinus, cosinus et tangente) ABC est un triangle rectangle en B. 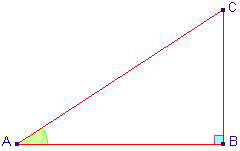
Le sinus de l'angle |
|
|
Le cosinus de l'angle
|
La tangente de l'angle
|
Au collège, sont introduites les notions de sinus, cosinus et tangentes. A
la différence de ce qui est fait
dans MATHilde Seconde, celles-ci ne se rapportent qu'à des angles
géométriques, c'est-à-dire des réels positifs.
En fait, on peut dire qu'en Seconde, on prolonge ce qui est fait au collège...
Sinus, cosinus et tangente d'un angle.
| Définition : (sinus, cosinus et tangente) ABC est un triangle rectangle en B. 
Le sinus de l'angle |
|
|
Le cosinus de l'angle
|
La tangente de l'angle
|
Remarque : il arrive que l'on parle du cosinus de
55°. En fait, c'est un abus de langage. Il serait plus correct de dire
"cosinus d'un angle de 55°".
Mais est-ce si important ?
Propriétés des sinus, cosinus et
tangente.
Ces trois fonctions présentent certaines propriétés que nous allons
énoncer :
En tant que rapport de deux longueurs, les sinus et cosinus
d'un angle sont des nombres positifs. Ils sont donc plus grand que 0.
De plus, dans un triangle rectangle, le plus grand côté est l'hypoténuse.
Les sinus et cosinus d'un angle sont donc plus petit que 1.
En conséquence :
| Propriété 1 : les sinus et cosinus d'un angle sont compris entre 0 et 1. |
| Propriété
2 : si ABC est un triangle rectangle en B alors :
|
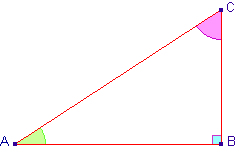 |
| Dans le cas ci-contre : Comme le triangle ABC est rectangle en B, alors en application du théorème de Pythagore : AB2 + BC2 = AC2 Ainsi :
|
 |
Propriété 3 : la
somme des carrés des sinus et cosinus d'un même angle est
égal à 1.
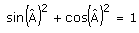 |
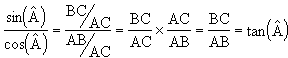
Propriété 4 : la tangente d'un angle est le quotient de ses sinus et cosinus.
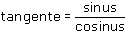 |