Après avoir défini les différents termes et
notions qui nous serons utiles, nous allons aborder les probabilités proprement
dites.
Probabilités : le commencement
Comme cela a été dit dans l'intro, les matheux
ont fait des probabilités une branche structurée à part entière des
mathématiques. Pour cela, ils ont défini la notion de loi
de probabilité. Voyons ce dont il s'agit.
Loi de probabilité.
Une loi de
probabilité est un mécanisme qui a un événement A fait
correspondre un nombre entre 0 et 1 : ce nombre est la probabilité qu'il se
produise.
Définition
d'une loi de probabilité.
E
est un ensemble sur lequel se déroule une épreuve
aléatoire.
Par exemple, le tirage d'une carte parmi un jeu E
de 32.
Une loi de
probabilité est une application p
(ou une fonction) qui à un événement fait correspondre un nombre
réel compris entre 0 et 1.
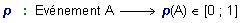
Cette loi de
probabilité vérifie les propriétés suivantes :
- p(E)
= 1
La probabilité de l'événement E (n'importe quelle carte
peut-être tirée) a une probabilité égale à 1.
- p(Æ
)
= 0
La probabilité de l'événement impossible Æ
(aucune carte ne peut convenir) a une probabilité égale à
0.
- Si A et B sont événements disjoints
alors p(A
ou B) = p(A) + p(B).
|
Il est très rare que l'on définisse
rigoureusement ce qu'est une loi de probabilité avant l'Université.
Généralement, on emploie le mot sans plus. Ce qui est important, c'est de
savoir calculer des probabilités comme dans les deux exemples que nous allons
voir.
Equiprobabilité : tirage
d'une carte parmi 32 autres.
Revenons à notre exemple de la première page : on tire au hasard une carte parmi un
jeu de 32.
C'est l'exemple type d'épreuve équiprobable
: chaque carte a la même probabilité d'être tirée.
| Quelle est la probabilité de Tirer
la dame de trèfle ?
Comme chaque carte a la même probabilité d'être tirée, qu'il y en a 32 alors
la probabilité de Tirer
la dame de trèfle est égale à 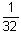 .
Autrement dit, une chance sur 32 de Tirer
la dame de trèfle. .
Autrement dit, une chance sur 32 de Tirer
la dame de trèfle. |
Formule
générale (équiprobabilité) :
S'il y a équiprobabilité alors la
probabilité d'un événement A est donnée par la formule :
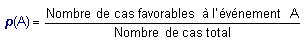
|
| Quelle est la probabilité de Tirer
une dame ?
Comme il y a quatre dames alors la probabilité de Tirer
une dame est de 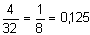 . .
En effet, il faut tirer l'une des quatre "bonnes" cartes à tirer
parmi les 32 présentes.
|
Remarque : En règle générale, on
préfère donner les probabilités sous la forme de fractions irréductibles.
C'est plus esthétique !
Nous reviendrons ultérieurement sur
cet exemple à l'occasion de l'avant-dernier paragraphe.
Non
équiprobabilité : exemple d'un dés pipé.
Idéalement, lorsque l'on lance un dés
bien équilibré, il y a équiprobabilité. C'est-à-dire que l'on a autant de
chance d'obtenir un deux qu'un quatre. Il en va différemment lorsque le dés
est pipé ou mal équilibré.
Dans cet
exemple, le dés ci-contre est mal équilibré.
L'épreuve aléatoire consiste à le lancer une fois. La loi de
probabilité de celle-ci est la suivante :
| Face |
1 |
2 |
3 |
4 |
5 |
6 |
| Probabilité |
0,2 |
0,1 |
0,3 |
0,1 |
0,2 |
0,1 |
Autrement écrit, la
probabilité d'obtenir un cinq au
lancer est de 0,2 ou de deux chances sur 10.
|
 |
| Quelle est la probabilité d'obtenir
un trois ?
En lisant le tableau, on lit que la probabilité d'obtenir un trois
est de 0,3 ou trois chances sur 10.
|
|
Quelle est la probabilité d'obtenir
un nombre paire ?
Les nombres paires que l'on peut obtenir en lançant un dés sont deux,
quatre et six.
L'événement nombre paire est donc
réalisé lorsque que l'on obtient un deux,
un quatre ou un six.
On pourrait résumer cela par :
nombre paire = deux ou quatre
ou six.
L'événement nombre paire est la réunion de ces trois événements
élémentaires.
Ainsi donc :
| p("nombre paire") |
= p("deux")
+ p("quatre")
+ p("six")
= 0,1 + 0,1 + 0,1
= 0,3 |
En conclusion, on a autant de chance
d'obtenir un trois qu'un nombre paire. |
| Mais comment qu'ils font leur loi de
probabilité ?
Pour obtenir la loi de probabilité du
dés, on se peut se servir de données statistiques.
C'est-à-dire que l'on lance un grand nombre de fois ce dés et à
chaque lancer, on note le nombre obtenu. A partir du tableau de
données, on a la probabilité d'obtenir par exemple un deux.
On peut aussi affiner les données en leur faisant subir toutes sortes
de traitements.
Un grand nombre d'expériences aléatoires permet donc de construire une
loi de probabilité.
|
Probabilité d'un
événement contraire.
Si l'on connaît la probabilité d'un événement A alors il est possible de
connaître la probabilité de l'événement contraire 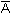 .
.
En effet, la réunion d'un événement A et de
son contraire 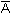 est
l'événement E = "n'importe
quoi fait l'affaire".
est
l'événement E = "n'importe
quoi fait l'affaire".
En effet, pour que A È
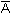 soit réalisé, il faut et il suffit que l'événement A soit réalisé ou que
son contraire le soit. Donc l'événement A È
soit réalisé, il faut et il suffit que l'événement A soit réalisé ou que
son contraire le soit. Donc l'événement A È
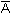 est toujours réalisé !
est toujours réalisé !
Ainsi, comme A È
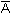 = E alors sa probabilité est égale à celle de E, c'est-à-dire 1.
= E alors sa probabilité est égale à celle de E, c'est-à-dire 1.
Comme de plus, les événements A et 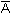 sont incompatibles alors en vertu de la troisième
propriété que respecte toute loi de probabilité digne de ce nom :
sont incompatibles alors en vertu de la troisième
propriété que respecte toute loi de probabilité digne de ce nom :
p(A
È
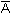 ) =
p( A)
+ p(
) =
p( A)
+ p(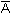 )
)
1 = p( A)
+ p(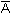 )
)
d'où
p(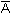 )
= 1 - p( A) )
= 1 - p( A) |
Un exemple d'application de cette propriété est
ce qui a été fait avec le jeu de cartes et l'événement Ne pas tirer un
pic.
Un autre exemple avec notre ami le dés
mal équilibré est ce qui suit :
| Quelle est la probabilité de ne
pas obtenir un trois ?
Cet événement est le contraire de
l'événement obtenir un trois.
Donc :
p("ne
pas obtenir un trois")
= 1 - p("obtenir
un trois") = 1 - 0,3
= 0,7.
On a donc deux fois de
chances de ne pas obtenir un trois que d'en avoir un. C'est bien de le
savoir ! |
Probabilités
d'une réunion et d'une intersection.
Lorsque que l'on connaît les probabilités des deux événements A
et B ainsi que celle de leur intersection A
et B, il est alors possible de connaître la probabilité de leur
réunion A ou B.
Formule liant les probabilités d'une réunion et d'une intersection :
Si A et B sont deux événements alors
p(A È B) = p(A) + p(B) - p(A Ç B)
Ce qui s'écrit encore :
p(A ou
B) = p(A) + p(B)
- p(A et B) |
Expliquons un peu d'où vient cette formule fort
belle mais peu utile :

Un exemple d'application de cette
propriété avec notre jeu de cartes est ce qui suit :
| Quelle est la probabilité de tirer
une dame ou un pic ?
L'événement tirer
une dame ou un pic est la réunion des événements tirer
une dame et tirer un pic.
Ces deux derniers étant de vieilles connaissances.
Leur intersection est l'événement tirer
la dame de pic.
La probabilité de leur intersection
est donc égale à 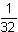 .
.
Ainsi donc :
| p("une
dame ou un pic") |
= p("une
dame")
+ p("un
pic")
+ p("la
dame de pic")
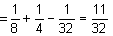 |
En conclusion, on a donc 11 chances sur
32 que la carte tirée soit une dame ou un pic. Une chose que l'on
savait déjà... |
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par
la taverne de l'Irlandais. A la mémoire de M. Couve de Murville(1907 - 1999).
(c) AMLTI Décembre 1999/Janvier 2003. Tous droits réservés.


