 |
La démonstration par récurrence est à la limite de tous les programmes de Première. Voilà une bonne raison d'en parler ! |
De
la démonstration par récurrence...
De quoi s'agit-il ?
Avant toute chose, nous allons dire ce qu'est un raisonnement par récurrence.
C'est quelque part ce qui suit :
 |
 |
 |
| |
Le raisonnement par récurrence
 |
Le raisonnement par récurrence s'apparente à la théorie des dominos :
|
On considère une suite de dominos.
Si un domino tombe alors le suivant tombera.
Comme le premier tombe alors le second tombera, puis le troisième, ...etc..
Conclusion : si le premier domino tombe alors tous tomberont.
| Tout repose en fait sur le principe de propagation "si l'un tombe alors le suivant aussi".
C'est une sorte de réaction en chaîne. Une seule étincelle, un seul domino qui tombe et tous seront par terre ! | Le raisonnement par récurrence comporte deux phases :
- prouver que le premier domino tombe.
- établir le principe : si le nième domino tombe alors le suivant (le numéro n+1) tombera..
Si on démontre ces deux choses alors la réaction se déclenche. Donc la propriété est démontrée pour tous les dominos !
Sauf qu'ici, un domino numéro n qui tombe est une propriété
ou une formule vraie au rang n.
| |
 |
 |
 |
A présent, nous allons le mettre en oeuvre sur quelques exemples.
Un premier exemple : démontrer une formule.
L'utilisation classique du raisonnement par récurrence est la démonstration d'une propriété d'une suite définie par récurrence...
 |  |  |
| |
On considère la suite (un) définie par :
u0 = 7 et pour tout entier n, un+1 = 2 × un - 3
Démontrons par récurrence que pour tout entier n, un = 2n+2 + 3.
|
Nous avons deux choses à démontrer.
- La formule est vraie au rang 0/Le premier domino tombe.
| Nous savons que : |
De plus : |
| u0 = 7. |
20+2 + 3 = 4 + 3 = 7 |
Donc pour n = 0, nous avons que : un = 2n+2 + 3.
La formule est donc vraie au rang 0. Le premier domino tombe.
- La formule se propage/Un domino qui tombe entraîne le suivant.
Supposons que la formule soit vraie à un rang n, c'est-à-dire que :
un = 2n+2 + 3.
Nous allons prouver qu'alors elle est vraie au rang n+1.
A ce stade, la seule chose que nous sachions sur un+1 est la relation qui le lie à un. On peut écrire que :
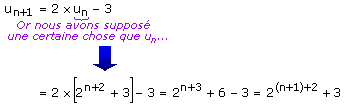
Donc la formule est alors aussi vraie au rang n+1. Donc elle se propage de rang en rang : un domino qui tombe, entraînera la chute du suivant...
La propriété est donc vraie au rang 0.
Le principe de propagation que nous avons établi, nous permet alors de dire que la propriété est alors vraie au rang 1, donc au rang 2, donc au rang 3,...
Tous les dominos tombent...
Conclusion : Pour tout entier naturel n, un = 2n+2 + 3.
|
| |
 |  |  |
Le truc en plus : mais comment qu'il a fait pour trouver sa formule ?
Le genre de suite que nous venons de traiter est ce que l'on appelle une suite récurrente linéaire. C'est une suite de la forme :
un+1 = a × un + b
Ne croyez pas que nous ayons trouvé l'expression de un en fonction de
n.
Non ! Tout cela repose d'un certain raisonnement en cascade.
Toute l'astuce consiste à écrire toutes les relations de récurrences entre un
et u0.
C'est l'histoire que vous narre l'animation suivante.

Ainsi donc pour tout entier naturel n :
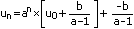
C'est ainsi et avec cette formule qu'une machine ou nous-même pouvons déterminer l'expression d'une suite récurrente linéaire en fonction de n.
|
D'autres exemples : les sommes de quelques choses.
Dans les pages précédentes, nous avons suggéré que certaines formules
comme celle donnant la somme des n premiers entiers pouvait être démontrée
par récurrence.
Voilà l'une des tâches à laquelle nous allons nous atteler dans ce paragraphe
: la récurrence à la rescousse de certaines sommes remarquables.
Mettons-nous au travail !
 |
 |
 |
| |
La somme des n premiers entiers : par récurrence
| Démontrons par récurrence que pour tout entier naturel non nul n,
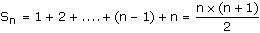
Cette formule a déjà été prouvée sans récurrence. |
Nous avons deux choses à démontrer. Alors au boulôt !
- La formule est vraie au rang 1/Le premier domino tombe.
| Nous savons que : |
De plus : |
| S1 = 1. |
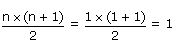 |
Ainsi pour n = 1, nous avons que :
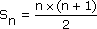 La formule est donc vraie au rang 1. La formule est donc vraie au rang 1.
- La formule se propage/Un domino qui tombe entraîne le suivant.
Supposons que la formule soit vraie à un rang n, c'est-à-dire que :
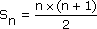
Nous allons prouver qu'alors elle est vraie au rang n+1.
A ce stade, la seule chose que nous sachions sur Sn+1 est qu'il est la somme des n+1 premiers entiers. Autrement dit :
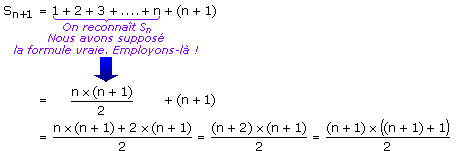
Donc la formule est alors vraie au rang n+1. Donc elle se propage de rang en rang
Conclusion : la somme des n premiers entiers est égale à
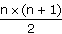 . .
|
| |
 |
 |
 |
 |
 |
 |
| |
La somme des n premiers entiers au carré : par récurrence
| Démontrons par récurrence que pour tout entier naturel non nul n,
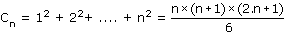
|
Nous avons deux choses à démontrer. Alors au boulôt !
- La formule est vraie au rang 1/Le premier domino tombe.
| Nous savons que : |
De plus : |
| C1 = 12 = 1. |
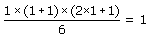 |
Ainsi pour n = 1, nous avons que :
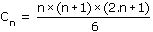 La formule est donc vraie au rang 1. La formule est donc vraie au rang 1.
- La formule se propage/Un domino qui tombe entraîne le suivant.
Supposons que la formule soit vraie au rang n, c'est-à-dire que :
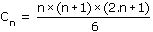
Nous allons prouver qu'alors elle est vraie au rang n+1.
A ce stade, la seule chose que nous sachions sur Cn+1 est qu'il est la somme des n+1 premiers entiers au carré. Autrement dit :
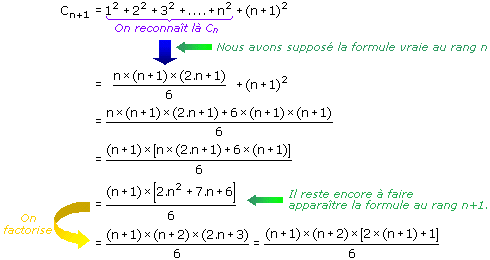
Donc la formule est alors vraie au rang n+1. Donc elle se propage de rang en rang
Conclusion : la somme des n premiers carrés est égale à
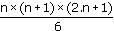 . .
|
| |
 |
 |
 |
 |
 |
 |
| |
La somme des n+1 premières puissances de q : par récurrence
q est ici un réel différent de 1.
Démontrons par récurrence que pour tout entier naturel n

Cette formule a déjà été démontrée sans récurrence. |
Différence avec ce qui précède : ici on part du rang 0.
Nous avons deux choses à démontrer. Alors au boulôt !
- La formule est vraie au rang 0/Le premier domino tombe.
| Nous savons que : |
De plus : |
| Q0 = q0 = 1. |
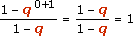 |
Ainsi pour n = 0, nous avons que :
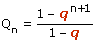 La formule est donc vraie au rang 0. La formule est donc vraie au rang 0.
- La formule se propage/Un domino qui tombe entraîne le suivant.
Supposons que la formule soit vraie au rang n, c'est-à-dire que :
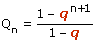
Nous allons prouver qu'alors elle est vraie au rang n+1.
A ce stade, la seule chose que nous sachions sur Qn+1 est qu'il est la somme des n+1 premières puissances de q. Autrement dit :
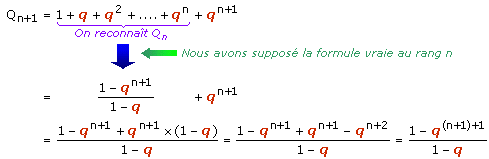
Donc la formule est alors vraie au rang n+1. Donc elle se propage de rang en rang.
Conclusion : la somme des n premières puissances de q est égale à
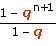 . .
|
| |
 |
 |
 |
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par
la taverne de l'Irlandais.
(c) AMLTI Décembre 2000/Janvier 2003. Tous droits réservés.
